segment (System Identification Toolbox)

Segment data and estimate models for each segment.

Syntax

segm = segment(z,nn) 
[segm,V,thm,R2e] = segment(z,nn,R2,q,R1,M,th0,P0,ll,mu)

Description

segment builds models of AR, ARX, or ARMAX/ARMA type,

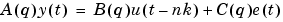
assuming that the model parameters are piece-wise constant over time. It results in a model that has split the data record into segments over which the model remains constant. The function models signals and systems that may undergo abrupt changes.

The input-output data are contained in z, which is either an iddata object or a matrix z = [y u] where y and u are column vectors. If the system has several inputs, u has the corresponding number of columns.

The argument nn defines the model order. For the ARMAX model

```
nn = [na nb nc nk]
```

where na, nb, and nc are the orders of the corresponding polynomials. See Polynomial Representation of Transfer Functions in the "Tutorial". Moreover nk is the delay. If the model has several inputs, nb and nk are row vectors, giving the orders and delays for each input.

For an ARX model (nc = 0) enter

```
nn = [na nb nk]
```

For an ARMA model of a time series

```
z = y
nn = [na nc]
```

and for an AR model

```
nn = na
```

The output argument segm is a matrix, whose k-row contains the parameters corresponding to time k. This is analogous to the output argument thm in rarx and rarmax. The output argument thm of segment contains the corresponding model parameters that have not yet been segmented. That is, they are not piecewise constant, and therefore correspond to the outputs of the functions rarmax and rarx. In fact, segment is an alternative to these two algorithms, and has a better capability to deal with time variations that may be abrupt.

The output argument V contains the sum of the squared prediction errors of the segmented model. It is a measure of how successful the segmentation has been.

The input argument R2 is the assumed variance of the innovations e(t) in the model. The default value of R2, R2 = [], is that it is estimated. Then the output argument R2e is a vector whose k-th element contains the estimate of R2 at time k.

The argument q is the probability that the model undergoes at an abrupt change at any given time. The default value is 0.01.

R1 is the assumed covariance matrix of the parameter jumps when they occur. The default value is the identity matrix with dimension equal to the number of estimated parameters.

M is the number of parallel models used in the algorithm (see below). Its default value is 5.

th0 is the initial value of the parameters. Its default is zero. P0 is the initial covariance matrix of the parameters. The default is 10 times the identity matrix.

ll is the guaranteed life of each of the models. That is, any created candidate model is not abolished until after at least ll time steps. The default is ll = 1. Mu is a forgetting parameter that is used in the scheme that estimates R2. The default is 0.97.

The most critical parameter for you to choose is R2. It is usually more robust to have a reasonable guess of R2 than to estimate it. Typically, you need to try different values of R2 and evaluate the results. (See the example below.) sqrt(R2) corresponds to a change in the value y(t) that is normal, giving no indication that the system or the input might have changed.

Algorithm

The algorithm is based on M parallel models, each recursively estimated by an algorithm of Kalman filter type. Each is updated independently, and its posterior probability is computed. The time varying estimate thm is formed by weighting together the M different models with weights equal to their posterior probability. At each time step the model (among those that have lived at least 11 samples) that has the lowest posterior probability is abolished. A new model is started, assuming that the system parameters have jumped, with probability q, a random jump from the most likely among the models. The covariance matrix of the parameter change is set to R1.

After all the data are examined, the surviving model with the highest posterior probability is tracked back and the time instances where it jumped are marked. This defines the different segments of the data. (If no models had been abolished in the algorithm, this would have been the maximum likelihood estimates of the jump instances.) The segmented model segm is then formed by smoothing the parameter estimate, assuming that the jump instances are correct. In other words, the last estimate over a segment is chosen to represent the whole segment.

Examples

Check how the algorithm segments a sinusoid into segments of constant levels. Then use a very simple model y(t) = b₁ * 1, where 1 is a fake input and 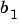describes the piecewise constant level of the signal y(t) (which is simulated as a sinusoid).

y = sin([1:50]/3)';
thm = segment([y,ones(y)],[0 1 1],0.1);
plot([thm,y])

By trying various values of R2 (0.1 in the above example), more levels are created as R2 decreases.

rplr selstruc