predict (System Identification Toolbox)

Predict the output k steps ahead.

Syntax

yp = predict(m,data)
[yp,mpred] = predict(m,data,k,init)

Description

data is the output-input data as an iddata object, and m is any idmodel object (idpoly, idss, idgrey, or idarx)

The argument k indicates that the k step ahead prediction of y according to the model m is computed. In the calculation of yp(t) the model can use outputs up to time

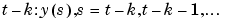
and inputs up to the current time t. The default value of k is 1.

The output yp is an iddata object containing the predicted values as OutputData. The output argument mpred contains the k-step ahead predictor. This is given as a cell array, whose k:th entry is an idpoly model for the predictor of output number k.

init determines how to deal with the initial state:

init ='estimate': The initial state is set to value that minimizes the norm of the prediction error associated with the model and the data.
init = 'zero' sets the initial state to zero.
init = 'model' used the model's internally stored initial state
init = x0, where x0 is a column vector of appropriate dimension uses that value as initial state

If init is not specified, the model property m.InitialState is used, so that 'Estimate', 'Backcast' and 'Auto' set init = 'Estimate', while m.InitialState = 'Zero' sets init = 'zero', and 'Model' and 'Fixed' set init = 'model'.

An important use of predict is to evaluate a model's properties in the mid-frequency range. Simulation with sim (which conceptually corresponds to k = inf) can lead to levels that drift apart, since the low frequency behavior is emphasized. One step ahead prediction is not a powerful test of the model's properties, since the high frequency behavior is stressed. The trivial predictor 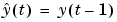can give good predictions in case the sampling of the data is fast.

Another important use of predict is to evaluate models of time series. The natural way of studying a time-series model's ability to reproduce observations is to compare its k-step ahead predictions with actual data.

Note that for Output-Error models, there is no difference between the k-step ahead predictions and the simulated output, since, by definition, Output-Error models only use past inputs to predict future outputs.

Algorithm

The model is evaluated in state-space form, and the state equations are simulated k-steps ahead with initial value 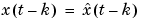, where 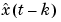is the Kalman filter state estimate.

Examples

Simulate a time series, estimate a model based on the first half of the data, and evaluate the four step ahead predictions on the second half.

m0 = idpoly([1 -0.99],[],[1 -1 0.2]);
e = iddata([],randn(400,1));
y = sim(m0,e);
m = armax(y(1:200),[1 2]);
yp = predict(m,y,4);
plot(y(201:400),yp(201:400))

Note that the last two commands also are achieved by

```
compare(y,m,4,201:400);
```

See Also

compare, sim, pe

plot (idmodepolydata) present