Tutorial (System Identification Toolbox)

System Identification Toolbox

Discrete and Continuous Time Models

Continuous-Time Models

Continuous-time models are created and recognized by the property 'Ts' = 0. All idmodel objects can be created and analyzed as continuous-time models by setting Ts equal to zero at the time of creation, as in

m = idpoly(1,[0 1 1],1,1,[1 2 3],'Ts',0)

for the model

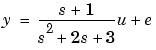
All model characteristics are then computed and graphed for the continuous-time representation. Time and frequency scales are determined using the sampling interval of the data, from which the model was estimated. For a nonestimated model, a default choice is made, which may make it necessary to supply frequency and time ranges to the commands.

For simulation and prediction, the continuous-time models are first converted to discrete time, using the sampling interval and intersample behavior of the data.

Estimating Continuous-Time Models

The estimation routines support the estimation of continuous-time state-space models in several different ways. The easiest is to use

```
mc = n4sid(Data,nx,'Ts',0)
```

This creates a continuous-time model in a free parameterization, based on the n4sid estimate. Further iterations from this estimate can be achieved by

```
mc = pem(Data,mc,'ss','can') 
```

or directly by

```
mc = pem(Data,nx,'Ts',0,'ss','can')
```

The search for the continuous-time model must be carried out in a canonical (or any other structured) parameterization. The fit is still made to the sampled signals in Data. The model is sampled with the data's sampling interval for the fit. The information about the input intersample behavior in Data. InterSample is used to determine whether the sampling should be zero-order-hold (zoh, piecewise constant input) or first-order-hold (foh, piecewise linear input). All this gives black-box state-space models without any prescribed internal structure. In these cases, and for a zoh input, it may be easier to first estimate a black-box model in discrete time and then transform it to continuous time with d2c as described below. For a foh input it might be better to directly estimate the continuous-time model, since the mapping from discrete to continuous under a foh assumption is somewhat tricky.

The major reason for identifying continuous-time model is to secure a particular structure of the continuous-time state-space matrices. This would typically reflect a physical interpretation or some greybox modeling work done. This situation is handled by defining the structure as a continuous time idss or idgrey model, as described inBlack-Box State-Space Models: the idss Model and onwards. The resulting structure mi is fitted to data in the usual way.

```
m = pem(Data,mi)
```

Transformations

Transformations between continuous-time and discrete-time model representations are achieved by c2d and d2c. Note that it is not sufficient to just assign a new value of Ts to the model object. The corresponding uncertainty measure (the estimated covariance matrix of the internal parameters) is also transformed in most cases. The syntax is

```
modc = d2c(modd)
modd = c2d(mc,T)
```

If the discrete-time model has some pure time delays (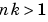) the default command removes them before forming the continuous-time model, and appends them using the property InputDelay in model modc. This property is used to add appropriate phase lag and shift the data, whenever the model is used. d2c also offers as an option to approximate the dead time by a finite dimensional system. Note that the disturbance properties are translated by the somewhat questionable formula (3-29). The covariance matrix is translated by Gauss' approximation formula using numerical derivatives. The M-file nuderst is then invoked. You may want to edit it for applications where the parameters have very different orders of magnitude. See the comments in State-Space Structures: Initial Values and Numerical Derivatives.

Here is an example that compares the Bode plots of an estimated model and its continuous-time counterpart.

m= armax(Data,[2 3 1 2]);
mc = d2c(m); bode(m,mc)

Transformations to Other Model Representations Model Structure Selection and Validation