Fixed-Point Blockset

Rounding

The result of any operation on a fixed-point number is typically stored in a register that is longer than the number's original format. When the result is put back into the original format, the extra bits must be disposed of. That is, the result must be rounded. Rounding involves going from high precision to lower precision and produces quantization errors and computational noise.

The blockset provides four rounding modes, which are shown in the expanded drop-down menu in the dialog below.

The Fixed-Point Blockset rounding modes are discussed below. The data is generated using the Simulink Signal Generator block and doubles are converted to signed 8-bit numbers with radix point-only scaling of 2^-2.

Round Toward Zero

The simplest rounding mode computationally is when all digits beyond the number required are dropped. This mode is referred to as rounding toward zero, and it results in a number whose magnitude is always less than or equal to the more precise original value. In MATLAB, you can round to zero using the fix function.

Rounding toward zero introduces a cumulative downward bias in the result for positive numbers and a cumulative upward bias in the result for negative numbers. That is, all positive numbers are rounded to smaller positive numbers, while all negative numbers are rounded to smaller negative numbers. Rounding toward zero is shown below.

An example comparing rounding to zero and truncation for unsigned and two's complement numbers appears in Example: Rounding to Zero Versus Truncation.

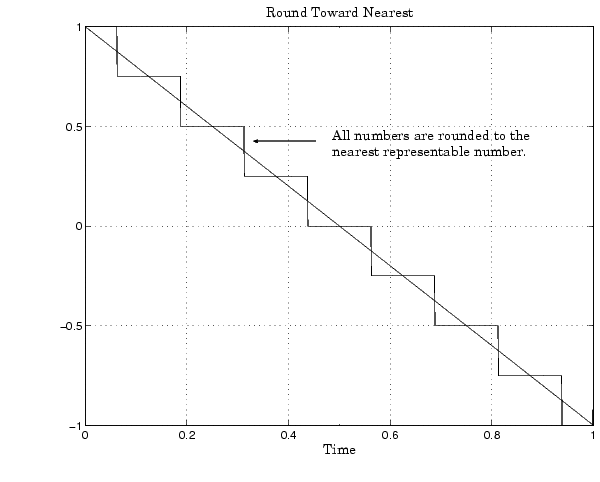
Round Toward Nearest

When you round toward nearest, the number is rounded to the nearest representable value. This mode has the smallest errors associated with it and these errors are symmetric. As a result, rounding toward nearest is the most useful approach for most applications.

In MATLAB, you can round to nearest using the round function. Rounding toward nearest is shown below.

Round Toward Ceiling

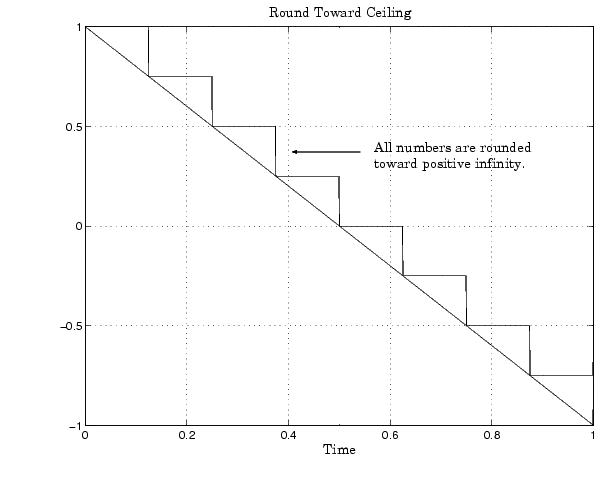
When you round toward ceiling, both positive and negative numbers are rounded toward positive infinity. As a result, a positive cumulative bias is introduced in the number.

In MATLAB, you can round to ceiling using the ceil function. Rounding toward ceiling is shown below.

Round Toward Floor

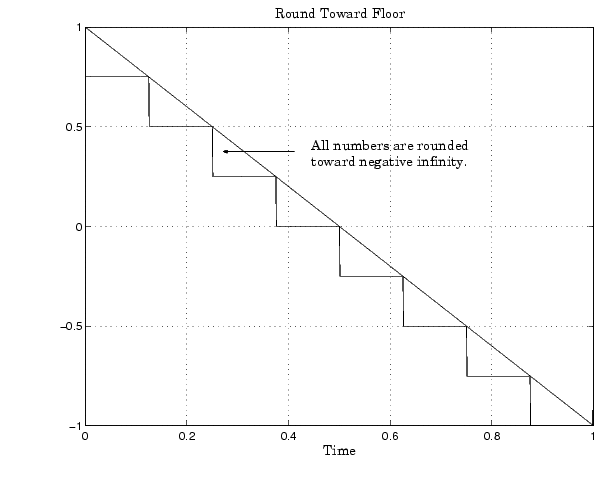
When you round toward floor, both positive and negative numbers are rounded to negative infinity. As a result, a negative cumulative bias is introduced in the number.

In MATLAB, you can round to floor using the floor function. Rounding toward floor is shown below.

Rounding toward ceiling and rounding toward floor are sometimes useful for diagnostic purposes. For example, after a series of arithmetic operations, you may not know the exact answer because of word-size limitations, which introduce rounding. If every operation in the series is performed twice, once rounding to positive infinity and once rounding to negative infinity, you obtain an upper limit and a lower limit on the correct answer. You can then decide if the result is sufficiently accurate or if additional analysis is required.

Example: Rounding to Zero Versus Truncation

Rounding to zero and truncation or chopping are sometimes thought to mean the same thing. However, the results produced by rounding to zero and truncation are different for unsigned and two's complement numbers.

To illustrate this point, consider rounding a 5-bit unsigned number to zero by dropping (truncating) the two least significant bits. For example, the unsigned number 100.01 = 4.25 is truncated to 100 = 4. Therefore, truncating an unsigned number is equivalent to rounding to zero or rounding to floor.

Now consider rounding a 5-bit two's complement number by dropping the two least significant bits. At first glance, you may think truncating a two's complement number is the same as rounding to zero. For example, dropping the last two digits of -3.75 yields -3.00. However, digital hardware performing two's complement arithmetic yields a different result. Specifically, the number 100.01 = -3.75 truncates to 100 = -4, which is rounding to floor.

As you can see, rounding to zero for a two's complement number is not the same as truncation when the original value is negative. For this reason, the ambiguous term "truncation" is not used in this guide, and four explicit rounding modes are used instead.

Limitations on Precision

Padding with Trailing Zeros