Fixed-Point Blockset

Gain

Consider the multiplication of a constant and a variable

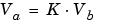
where K is a constant called the gain. Since V_a results from the multiplication of a constant and a variable, finding Q_a is a simplified version of the general fixed-point multiply formula:

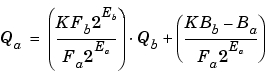
Note that the terms in the parentheses can be calculated offline. Therefore, there is only one multiplication of a constant and a variable and one addition.

To implement the above equation without changing it to a more complicated form, the constants need to be encoded using a radix point-only format. For each of these constants, the range is the trivial case of only one value. Despite the trivial range, the radix point formulas for maximum precision are still valid. The maximum precision representations are the most useful choices unless there is an overriding need to avoid any shifting. The encoding of the constants is

resulting in the formula

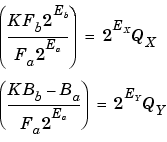
Inherited Scaling for Speed

The number of arithmetic operations can be reduced with these choices:

• Set B_a = KB_b. This eliminates one constant term.
• Set F_a = KF_b and E_a = E_b. This sets the other constant term to unity.

  The resulting formula is simply

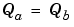
If the number of bits is different, then either handling potential overflows or performing sign extensions is the only possible operations involved.

Inherited Scaling for Maximum Precision

The scaling for maximum precision does not need to be different than the scaling for speed unless the output has fewer bits than the input. If this is the case, then saturation should be avoided by dividing the slope by 2 for each lost bit. This will prevent saturation but will cause rounding to occur.

Multiplication

Division