| Fixed-Point Blockset | |
Floating-Point Numbers
Fixed-point numbers are limited in that they cannot simultaneously represent very large or very small numbers using a reasonable word size. This limitation can be overcome by using scientific notation. With scientific notation, you can dynamically place the radix point at a convenient location and use powers of the radix to keep track of that location. Thus, you can represent a range of very large and very small numbers with only a few digits.
You can represent any binary floating-point number in scientific notation form as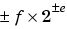 
where f is the fraction (or mantissa); 2 is the radix or base (binary in this case); and e is the exponent of the radix. The radix is always a positive number while f and e can be positive or negative.
When performing arithmetic operations, floating-point hardware must take into account that the sign, exponent, and fraction are all encoded within the same binary word. This results in complex logic circuits when compared with the circuits for binary fixed-point operations.
The Fixed-Point Blockset supports single-precision and double-precision floating-point numbers as defined by the IEEE Standard 754. Additionally, a nonstandard IEEE-style number is supported. To link the world of fixed-point numbers with the world of floating-point numbers, the concepts behind scientific notation are reviewed below.
| | Example: Constant Scaling for Best Precision | Scientific Notation | |