Fixed-Point Blockset

Simulation Results

The results of two simulation trials are given below. The first trial uses radix point-only scaling while the second trial uses [Slope Bias] scaling.

Trial 1: Radix Point-Only Scaling

When using radix point-only scaling, your goal is to find the optimal power-of-two exponent E, as defined in Selecting the Output Scaling. For this scaling mode, the fractional slope F is set to 1 and no bias is required.

The Gateway In block is configured in this way:

• Output data type

• The output data type is given by sfix(5). This creates a MATLAB structure that is a 5-bit, signed generalized fixed-point number.

• Output scaling

• The output scaling is given by 2^-2, which puts the radix point two places to the left of the rightmost bit. This gives a maximum value of 011.11 = 3.75, a minimum value of 100.00 = -4.00, and a precision of (1/2)² = 0.25.

• Rounding

• The rounding mode is given by Nearest. This rounds the fixed-point result to the nearest representable number, with the exact midpoint rounded towards positive infinity.

• Overflows

• Fixed-point values that overflow will saturate to the maximum or minimum value represented by the word.

The resulting real-world and fixed-point simulation results are shown below.

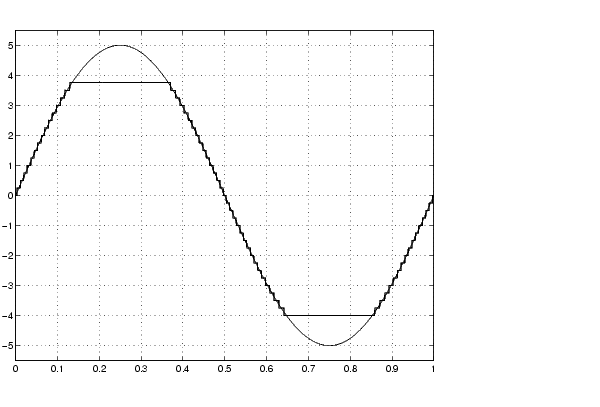
The simulation clearly demonstrates the quantization effects of fixed-point arithmetic. The combination of using a 5-bit word with a precision of (1/2)² = 0.25 produces a discretized output that does not span the full range of the input signal.

If you want to span the complete range of the input signal with 5 bits using radix point-only scaling, then your only option is to sacrifice precision. Hence, the output scaling would be given by 2^-1, which puts the radix point one place to the left of the rightmost bit. This scaling gives a maximum value of 0111.1 = 7.5, a minimum value of 1000.0 = -8.0, and a precision of (1/2)¹ = 0.5.

Trial 2: [Slope Bias] Scaling

When using [Slope Bias] scaling, your goal is to find the optimal fractional slope F and fixed power-of-two exponent E, as defined in Selecting the Output Scaling. No bias is required for this example since the sine wave is defined on the interval [-5 5]. The Gateway In block configuration is the same as that of the previous trial except for the scaling.

To arrive at a value for the slope, you can begin by assuming a fixed power-of- two exponent of -2. In the previous trial, this value defined the radix point-only scaling and resulted in a precision of 0.25. To find the fractional slope, you divide the maximum value of the sine wave by the maximum value of the scaled 5-bit number. The result is 5.00/3.75 = 1.3333. The slope (and precision) is 1.3333.(0.25) = 0.3333. You specify this value as [0.3333] for the Output scaling parameter.

Of course, you could have specified a fixed power-of-two exponent of -1 and a corresponding fractional slope of 0.6667. Naturally, the resulting slope is the same since E was reduced by one bit but F was increased by one bit. In this case, the blockset would automatically store F as 1.3332 and E as -2 due to the normalization condition of .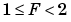

The resulting real-world and fixed-point simulation results are shown below.

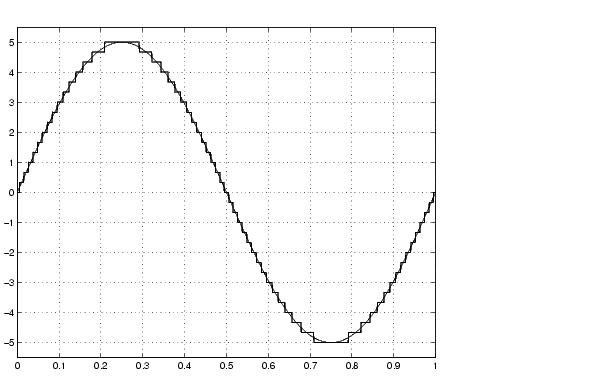
This somewhat cumbersome process used to find the slope is not really necessary. All that is required is the range of the data you are simulating and the size of the fixed-point word used in the simulation. In general, you can achieve reasonable simulation results by selecting your scaling based on the formula

where

• max is the maximum value to be simulated.
• min is the minimum value to be simulated.
• ws is the word size in bits.
• 2^ws - 1 is the largest value of a word with whose size is given by ws.

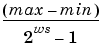
For this example, the formula produces a slope of 0.32258.

Block Descriptions

Demos