| Function Reference | |
Compute canonical state-space realizations
Syntax
Description
canon computes a canonical state-space model for the continuous or discrete LTI system sys. Two types of canonical forms are supported.
Modal Form
csys = canon(sys,'type') returns a realization csys in modal form, that is, where the real eigenvalues appear on the diagonal of the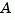 
matrix and the complex conjugate eigenvalues appear in 2-by-2 blocks on the diagonal of 
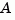. For a system with eigenvalues 
, the modal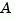 
matrix is of the form
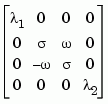
Companion Form
csys = canon(sys,'type') produces a companion realization of sys where the characteristic polynomial of the system appears explicitly in the rightmost column of the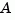 
matrix. For a system with characteristic polynomial
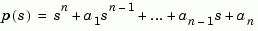
the corresponding companion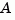 
matrix is
also returns the state coordinate transformation T relating the original state vector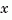 
and the canonical state vector 
.
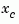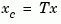
This syntax returns T=[] when sys is not a state-space model.
Algorithm
Transfer functions or zero-pole-gain models are first converted to state space using ss.
The transformation to modal form uses the matrix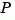 
of eigenvectors of the 
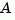matrix. The modal form is then obtained as
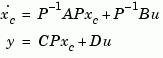
The state transformation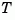 
returned is the inverse of 
.
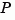The reduction to companion form uses a state similarity transformation based on the controllability matrix [1].
Limitations
The modal transformation requires that the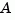 
matrix be diagonalizable. A sufficient condition for diagonalizability is that 
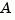has no repeated eigenvalues.
The companion transformation requires that the system be controllable from the first input. The companion form is often poorly conditioned for most state-space computations; avoid using it when possible.
See Also
ctrb Controllability matrix
ctrbf Controllability canonical form
ss2ss State similarity transformation
References
[1] Kailath, T. Linear Systems, Prentice-Hall, 1980.
| | c2d | care | |