Reliable Computations

Numerical Stability

Numerical stability is somewhat more difficult to illustrate meaningfully. Consult the references in [5], [6], and [7] for further details. Here is one small example to illustrate the difference between stability and conditioning.

Gaussian elimination with no pivoting for solving the linear system 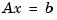is known to be numerically unstable. Consider

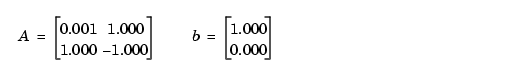
All computations are carried out in three-significant-figure decimal arithmetic. The true answer 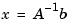is approximately

Using row 1 as the pivot row (i.e., subtracting 1000 times row 1 from row 2) you arrive at the equivalent triangular system.

Note that the coefficient multiplying 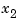in the second equation should be 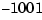, but because of roundoff, becomes 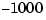. As a result, the second equation yields 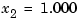, a good approximation, but now back-substitution in the first equation

yields 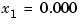. This extremely bad approximation of 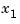is the result of numerical instability. The problem itself can be shown to be quite well-conditioned. Of course, MATLAB implements Gaussian elimination with pivoting.

Conditioning and Numerical Stability

Choice of LTI Model