Conditioning and Numerical Stability (Reliable Computations)

Reliable Computations

Conditioning and Numerical Stability

Two of the key concepts in numerical analysis are the conditioning of problems and the stability of algorithms.

Conditioning

Consider the linear system 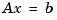given by

A =
    0.7800    0.5630
    0.9130    0.6590
b =
    0.2170
    0.2540

The true solution is x = [1, -1]' and you can calculate it approximately using MATLAB.

x = A\b
x =
     1.0000
    -1.0000

format long, x
x =
     0.99999999991008
    -0.99999999987542

Of course, in real problems you almost never have the luxury of knowing the true solution. This problem is very ill-conditioned. To see this, add a small perturbation to A

E =
     0.0010     0.0010
    -0.0020    -0.0010

and solve the perturbed system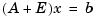

xe = (A+E)\b
xe =
    -5.0000
     7.3085

Notice how much the small change in the data is magnified in the solution.

One way to measure the magnification factor is by means of the quantity

called the condition number of 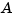with respect to inversion. The condition number determines the loss in precision due to roundoff errors in Gaussian elimination and can be used to estimate the accuracy of results obtained from matrix inversion and linear equation solution. It arises naturally in perturbation theories that compare the perturbed solution 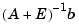with the true solution .

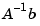In MATLAB, the function cond calculates the condition number in 2-norm. cond(A) is the ratio of the largest singular value of A to the smallest. Try it for the example above. The usual rule is that the exponent log10(cond(A)) on the condition number indicates the number of decimal places that the computer can lose to roundoff errors.

IEEE standard double precision numbers have about 16 decimal digits of accuracy, so if a matrix has a condition number of 10¹⁰, you can expect only six digits to be accurate in the answer. If the condition number is much greater than 1/sqrt(eps), caution is advised for subsequent computations. For IEEE arithmetic, the machine precision, eps, is about 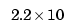^-16, and 1/sqrt(eps) = 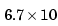⁸.

Another important aspect of conditioning is that, in general, residuals are reliable indicators of accuracy only if the problem is well-conditioned. To illustrate, try computing the residual vector 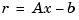for the two candidate solutions x = [0.999 -1.001]' and x = [0.341 -0.087]'. Notice that the second, while clearly a much less accurate solution, gives a far smaller residual. The conclusion is that residuals are unreliable indicators of relative solution accuracy for ill-conditioned problems. This is a good reason to be concerned with computing or estimating accurately the condition of your problem.

Another simple example of an ill-conditioned problem is the 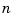-by-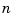 matrix with ones on the first upper-diagonal.

```
A = diag(ones(1,n-1),1);
```

This matrix has 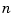eigenvalues at 0. Now consider a small perturbation of the data consisting of adding the number 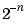to the first element in the last (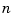th) row of A. This perturbed matrix has n distinct eigenvalues 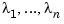with

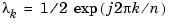. Thus, you can see that this small perturbation in the data has been magnified by a factor on the order of 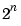to result in a rather large perturbation in the solution (the eigenvalues of A). Further details and related examples are to be found in [7].

It is important to realize that a matrix can be ill-conditioned with respect to inversion but have a well-conditioned eigenproblem, and vice versa. For example, consider an upper triangular matrix of ones (zeros below the diagonal) given by

```
A = triu(ones(n));
```

This matrix is ill-conditioned with respect to its eigenproblem (try small perturbations in A(n,1) for, say, n=20), but is well-conditioned with respect to inversion (check its condition number). On the other hand, the matrix

has a well-conditioned eigenproblem, but is ill-conditioned with respect to inversion for small .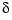

Reliable Computations Numerical Stability