Creating and Manipulating Models

Discrete-Time Models

Creating discrete-time models is very much like creating continuous-time models, except that you must also specify a sampling period or sample time for discrete-time models. The sample time value should be scalar and expressed in seconds. You can also use the value -1 to leave the sample time unspecified.

To specify discrete-time LTI models using tf, zpk, ss, or frd, simply append the desired sample time value Ts to the list of inputs.

• sys1 = tf(num,den,Ts)
  sys2 = zpk(z,p,k,Ts)
  sys3 = ss(a,b,c,d,Ts)
  sys4 = frd(response,frequency,Ts)
  

For example,

• h = tf([1 -1],[1 -0.5],0.1)
  

creates the discrete-time transfer function

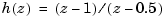with sample time 0.1 seconds, and

• sys = ss(A,B,C,D,0.5)
  

specifies the discrete-time state-space model

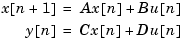
with sampling period 0.5 second. The vectors 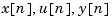denote the values of the state, input, and output vectors at the nth sample.

By convention, the sample time of continuous-time models is Ts = 0. Setting Ts = -1 leaves the sample time of a discrete-time model unspecified. For example,

• h = tf([1 -0.2],[1 0.3],-1)
  

produces

• Transfer function:
  z - 0.2
  -------
  z + 0.3
   
  Sampling time: unspecified
  

Note    Do not simply omit Ts in this case. This would make h a continuous-time transfer function.

If you forget to specify the sample time when creating your model, you can still set it to the correct value by reassigning the LTI property Ts. See Sample Time for more information on setting this property.

Discrete-Time TF and ZPK Models

You can specify discrete-time TF and ZPK models using tf and zpk as indicated above. Alternatively, it is often convenient to specify such models by:

1. Defining the variable z as a particular discrete-time TF or ZPK model with the appropriate sample time
2. Entering your TF or ZPK model directly as a rational expression in z.

This approach parallels the procedure for specifying continuous-time TF or ZPK models using rational expressions. This procedure is described in SISO Transfer Function Models and SISO Zero-Pole-Gain Models.

For example,

• z = tf('z', 0.1);
  H = (z+2)/(z^2 + 0.6*z + 0.9);
  

creates the same TF model as

• H = tf([1 2], [1 0.6 0.9], 0.1);
  

Similarly,

• z = zpk('z', 0.1);
  H = [z/(z+0.1)/(z+0.2) ; (z^2+0.2*z+0.1)/(z^2+0.2*z+0.01)]
  

produces the single-input, two-output ZPK model

• Zero/pole/gain from input to output...
               z
   #1:  ---------------
        (z+0.1) (z+0.2)
   
        (z^2 + 0.2z + 0.1)
   #2:  ------------------
            (z+0.1)^2
   
  Sampling time: 0.1
  

Note that:

• The syntax z = tf('z') is equivalent to z = tf('z',-1) and leaves the sample time unspecified. The same applies to z = zpk('z').
• Once you have defined z as indicated above, any rational expressions in z creates a discrete-time model of the same type and with the same sample time as z.

Discrete Transfer Functions in DSP Format

In digital signal processing (DSP), it is customary to write discrete transfer functions as rational expressions in 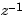and to order the numerator and denominator coefficients in ascending powers of 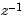. For example, the numerator and denominator of

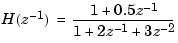
would be specified as the row vectors [1 0.5] and [1 2 3], respectively. When the numerator and denominator have different degrees, this convention clashes with the "descending powers of 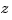" convention assumed by tf (see Transfer Function Models, or tf). For example,

• h = tf([1 0.5],[1 2 3])
  

produces the transfer function

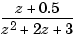
which differs from 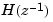by a factor .

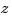To avoid such convention clashes, the Control System Toolbox offers a separate function filt dedicated to the DSP-like specification of transfer functions. Its syntax is

• h = filt(num,den)
  

for discrete transfer functions with unspecified sample time, and

• h = filt(num,den,Ts)
  

to further specify the sample time Ts. This function creates TF objects just like tf, but expects num and den to list the numerator and denominator coefficients in ascending powers of 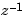. For example, typing

• h = filt([1 0.5],[1 2 3])
  

produces

• Transfer function:
     1 + 0.5 z^-1
  -------------------
  1 + 2 z^-1 + 3 z^-2
   
  Sampling time: unspecified
  

You can also use filt to specify MIMO transfer functions in 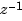. Just as for tf, the input arguments num and den are then cell arrays of row vectors of appropriate dimensions (see Transfer Function Models for details). Note that each row vector should comply with the "ascending powers of 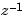" convention.

Frequency Response Data (FRD) Models

Data Retrieval