Design Case Studies

Root Locus Design

A reasonable design objective is to provide a damping ration 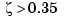with a natural frequency 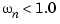rad/sec. Since the simplest compensator is a static gain, first try to determine appropriate gain values using the root locus technique.

• % Plot the root locus for the rudder to yaw channel
  rlocus(sys11)
  
  
  
  

This is the root locus for negative feedback and shows that the system goes unstable almost immediately. If, instead, you use positive feedback, you may be able to keep the system stable.

• rlocus(-sys11)
  sgrid
  
  
  
  

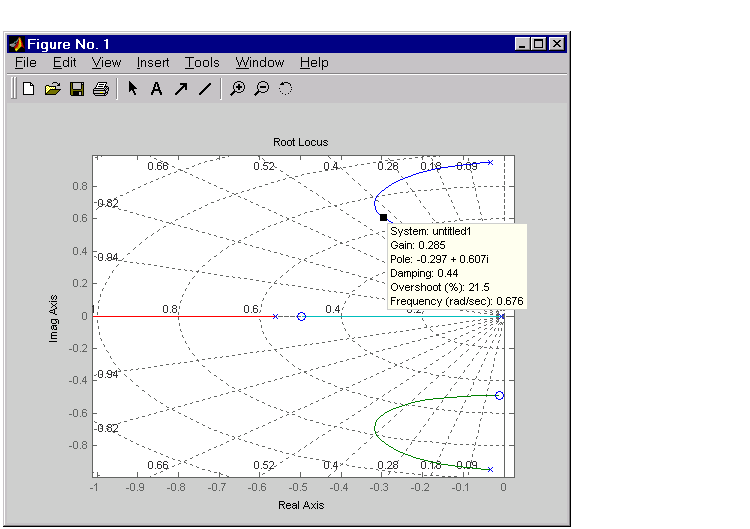
This looks better. By using simple feedback, you can achieve a damping ratio of 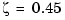. Click on the blue curve and move the data marker to track the gain and damping values. To achieve a 0.45 damping ratio, the gain should be about 2.85. This figure shows the data marker with similar values.

Next, close the SISO feedback loop.

• K = 2.85;
  cl11 = feedback(sys11,-K);   % Note: feedback assumes negative 
                               % feedback by default
  

Plot the closed-loop impulse response for a duration of 20 seconds, and compare it to the open-loop impulse response.

• impulse(sys11,'b--',cl11,'r',20)
  
  
  
  

The closed-loop response settles quickly and does not oscillate much, particularly when compared to the open-loop response.

Now close the loop on the full MIMO model and see how the response from the aileron looks. The feedback loop involves input 1 and output 1 of the plant (use feedback with index vectors selecting this input/output pair). At the MATLAB prompt, type

• cloop = feedback(sys,-K,1,1);
  damp(cloop)    % closed-loop poles
  Eigenvalue            Damping     Freq. (rad/s)  
  
  -3.42e-001                  1.00e+000      3.42e-001    
  -2.97e-001 + 6.06e-001i     4.40e-001      6.75e-001    
  -2.97e-001 - 6.06e-001i     4.40e-001      6.75e-001    
  -1.05e+000                  1.00e+000      1.05e+000 
  

Plot the MIMO impulse response.

• impulse(sys,'b--',cloop,'r',20)
  
  
  
  

The yaw rate response is now well damped, but look at the plot from aileron (input 2) to bank angle (output 2). When you move the aileron, the system no longer continues to bank like a normal aircraft. You have over-stabilized the spiral mode. The spiral mode is typically a very slow mode and allows the aircraft to bank and turn without constant aileron input. Pilots are used to this behavior and will not like your design if it does not allow them to fly normally. This design has moved the spiral mode so that it has a faster frequency.

Open-Loop Analysis

Washout Filter Design