

| MATLAB Function Reference |   |
Find zero of a function of one variable
Syntax
x = fzero(fun,x0) x = fzero(fun,x0,options) x = fzero(fun,x0,options,P1,P2,...) [x,fval] = fzero(...) [x,fval,exitflag] = fzero(...) [x,fval,exitflag,output] = fzero(...)
Description
x = fzero(fun,x0)
tries to find a zero of fun near x0, if x0 is a scalar. The value x returned by fzero is near a point where fun changes sign, or NaN if the search fails. In this case, the search terminates when the search interval is expanded until an Inf, NaN, or complex value is found.
If x0 is a vector of length two, fzero assumes x0 is an interval where the sign of fun(x0(1)) differs from the sign of fun(x0(2)). An error occurs if this is not true. Calling fzero with such an interval guarantees fzero will return a value near a point where fun changes sign.
x = fzero(fun,x0,options)
minimizes with the optimization parameters specified in the structure options. You can define these parameters using the optimset function. fzero uses these options structure fields:
x = fzero(fun,x0,options,P1,P2,...)
provides for additional arguments passed to the function, fun. Use options = [] as a placeholder if no options are set.
[x,fval] = fzero(...)
returns the value of the objective function fun at the solution x.
[x,fval,exitflag] = fzero(...)
returns a value exitflag that describes the exit condition of fzero:
[x,fval,exitflag,output] = fzero(...)
returns a structure output that contains information about the optimization:
output.algorithm |
The algorithm used |
output.funcCount |
The number of function evaluations |
output.iterations |
The number of iterations taken |
| Note For the purposes of this command, zeros are considered to be points where the function actually crosses, not just touches, the x-axis. |
Arguments
fun is the function whose zero is to be computed. It accepts a vector x and returns a scalar f, the objective function evaluated at x. The function fun can be specified as a function handle.
where myfun is a MATLAB function such as
fun can also be an inline object.
Other arguments are described in the syntax descriptions above.
Examples
Example 1. Calculate 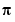 by finding the zero of the sine function near 3.
by finding the zero of the sine function near 3.
Example 2. To find the zero of cosine between 1 and 2
Note that cos(1) and cos(2) differ in sign.
Example 3. To find a zero of the function 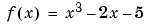
Because this function is a polynomial, the statement roots([1 0 -2 -5]) finds the same real zero, and a complex conjugate pair of zeros.
Algorithm
The fzero command is an M-file. The algorithm, which was originated by T. Dekker, uses a combination of bisection, secant, and inverse quadratic interpolation methods. An Algol 60 version, with some improvements, is given in [1]. A Fortran version, upon which the fzero M-file is based, is in [2].
Limitations
The fzero command finds a point where the function changes sign. If the function is continuous, this is also a point where the function has a value near zero. If the function is not continuous, fzero may return values that are discontinuous points instead of zeros. For example, fzero(@tan,1) returns 1.5708, a discontinuous point in tan.
Furthermore, the fzero command defines a zero as a point where the function crosses the x-axis. Points where the function touches, but does not cross, the x-axis are not valid zeros. For example, y = x.^2 is a parabola that touches the x-axis at 0. Because the function never crosses the x-axis, however, no zero is found. For functions with no valid zeros, fzero executes until Inf, NaN, or a complex value is detected.
See Also
roots, fminbnd, function_handle (@), inline, optimset
References
[1] Brent, R., Algorithms for Minimization Without Derivatives, Prentice-Hall, 1973.
[2] Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.
 | fwrite (serial) | gallery |  |