MATLAB Function Reference

fminsearch

Minimize a function of several variables

Syntax

• x = fminsearch(fun,x0)
  x = fminsearch(fun,x0,options)
  x = fminsearch(fun,x0,options,P1,P2,...)
  [x,fval] = fminsearch(...)
  [x,fval,exitflag] = fminsearch(...)
  [x,fval,exitflag,output] = fminsearch(...)
  

Description

fminsearch finds the minimum of a scalar function of several variables, starting at an initial estimate. This is generally referred to as unconstrained nonlinear optimization.

x = fminsearch(fun,x0) starts at the point x0 and finds a local minimum x of the function described in fun. x0 can be a scalar, vector, or matrix.

x = fminsearch(fun,x0,options) minimizes with the optimization parameters specified in the structure options. You can define these parameters using the optimset function. fminsearch uses these options structure fields:

Display	Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' displays just the final output; 'notify' (default) dislays output only if the function does not converge.
MaxFunEvals	Maximum number of function evaluations allowed.
MaxIter	Maximum number of iterations allowed.
TolX	Termination tolerance on x.

x = fminsearch(fun,x0,options,P1,P2,...) passes the problem-dependent parameters P1, P2, etc., directly to the function fun. Use options = [] as a placeholder if no options are set.

[x,fval] = fminsearch(...) returns in fval the value of the objective function fun at the solution x.

[x,fval,exitflag] = fminsearch(...) returns a value exitflag that describes the exit condition of fminsearch:

>0	Indicates that the function converged to a solution x.
0	Indicates that the maximum number of function evaluations was exceeded.
<0	Indicates that the function did not converge to a solution.

[x,fval,exitflag,output] = fminsearch(...) returns a structure output that contains information about the optimization:

output.algorithm	The algorithm used
output.funcCount	The number of function evaluations
output.iterations	The number of iterations taken

Arguments

fun is the function to be minimized. It accepts an input x and returns a scalar f, the objective function evaluated at x. The function fun can be specified as a function handle.

• x = fminsearch(@myfun,x0,A,b)
  

where myfun is a MATLAB function such as

• function f = myfun(x)
  f = ...            % Compute function value at x
  

fun can also be an inline object.

• x = fminsearch(inline('sin(x*x)'),x0,A,b);
  

Other arguments are described in the syntax descriptions above.

Examples

A classic test example for multidimensional minimization is the Rosenbrock banana function

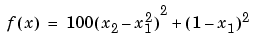
The minimum is at (1,1) and has the value 0. The traditional starting point is (-1.2,1). The M-file banana.m defines the function.

• function f = banana(x)
  f = 100*(x(2)-x(1)^2)^2+(1-x(1))^2;
  

The statement

• [x,fval] = fminsearch(@banana,[-1.2, 1])
  

produces

• x =
  
      1.0000    1.0000
  
  fval =
  
      8.1777e-010
  

This indicates that the minimizer was found to at least four decimal places with a value near zero.

Move the location of the minimum to the point [a,a^2] by adding a second parameter to banana.m.

• function f = banana(x,a)
  if nargin < 2, a = 1; end
  f = 100*(x(2)-x(1)^2)^2+(a-x(1))^2;
  

Then the statement

• [x,fval] = fminsearch(@banana, [-1.2, 1], ...
     optimset('TolX',1e-8), sqrt(2));
  

sets the new parameter to sqrt(2) and seeks the minimum to an accuracy higher than the default on x.

Algorithm

fminsearch uses the simplex search method of [1]. This is a direct search method that does not use numerical or analytic gradients.

If n is the length of x, a simplex in n-dimensional space is characterized by the n+1 distinct vectors that are its vertices. In two-space, a simplex is a triangle; in three-space, it is a pyramid. At each step of the search, a new point in or near the current simplex is generated. The function value at the new point is compared with the function's values at the vertices of the simplex and, usually, one of the vertices is replaced by the new point, giving a new simplex. This step is repeated until the diameter of the simplex is less than the specified tolerance.

Limitations

fminsearch can often handle discontinuity, particularly if it does not occur near the solution. fminsearch may only give local solutions.

fminsearch only minimizes over the real numbers, that is, 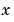must only consist of real numbers and 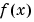must only return real numbers. When 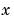has complex variables, they must be split into real and imaginary parts.

See Also

fminbnd, optimset, function_handle (@), inline

References

[1]  Lagarias, J.C., J. A. Reeds, M. H. Wright, and P. E. Wright, "Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions," SIAM Journal of Optimization, Vol. 9 Number 1, pp. 112-147, 1998.

fmins

fopen