

| Mathematics |   |
Interpolation and Multidimensional Arrays
Several interpolation functions operate specifically on multidimensional data.
| Function |
Description |
|
Three-dimensional data interpolation. |
|
Multidimensional data interpolation. |
|
Multidimensional data gridding (ndfun directory). |
Interpolation of Three-Dimensional Data
The function interp3 performs three-dimensional interpolation, finding interpolated values between points of a three-dimensional set of samples V. You must specify a set of known data points:
X, Y, and Z matrices specify the points for which values of V are given.
V contains values corresponding to the points in X, Y, and Z.
The most general form for interp3 is
XI, YI, and ZI are the points at which interp3 interpolates values of V. For out-of-range values, interp3 returns NaN.
There are three different interpolation methods for three-dimensional data:
method = 'nearest'). This method chooses the value of the nearest point.
method = 'linear'). This method uses piecewise linear interpolation based on the values of the nearest eight points.
method = 'cubic'). This method uses piecewise cubic interpolation based on the values of the nearest sixty-four points.
All of these methods require that X, Y, and Z be monotonic, that is, either always increasing or always decreasing in a particular direction. In addition, you should prepare these matrices using the meshgrid function, or else be sure that the "pattern" of the points emulates the output of meshgrid.
Each method automatically maps the input to an equally spaced domain before interpolating. If x is already equally spaced, you can speed execution time by prepending an asterisk to the method string, for example, '*cubic'.
Interpolation of Higher Dimensional Data
The function interpn performs multidimensional interpolation, finding interpolated values between points of a multidimensional set of samples V. The most general form for interpn is
1, 2, 3, ... are matrices that specify the points for which values of V are given. V is a matrix that contains the values corresponding to these points. 1, 2, 3, ... are the points for which interpn returns interpolated values of V. For out-of-range values, interpn returns NaN.
Y1, Y2, Y3, ... must be either arrays of the same size, or vectors. If they are vectors of different sizes, interpn passes them to ndgrid and then uses the resulting arrays.
There are three different interpolation methods for multidimensional data:
method = 'nearest'). This method chooses the value of the nearest point.
method = 'linear'). This method uses piecewise linear interpolation based on the values of the nearest two points in each dimension.
method = 'cubic'). This method uses piecewise cubic interpolation based on the values of the nearest four points in each dimension.
All of these methods require that X1, X2,X3 be monotonic. In addition, you should prepare these matrices using the ndgrid function, or else be sure that the "pattern" of the points emulates the output of ndgrid.
Each method automatically maps the input to an equally spaced domain before interpolating. If X is already equally spaced, you can speed execution time by prepending an asterisk to the method string; for example, '*cubic'.
Multidimensional Data Gridding
The ndgrid function generates arrays of data for multidimensional function evaluation and interpolation. ndgrid transforms the domain specified by a series of input vectors into a series of output arrays. The ith dimension of these output arrays are copies of the elements of input vector xi.
For example, assume that you want to evaluate a function of three variables over a given range. Consider the function
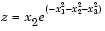
for 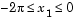 ,
, 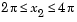 , and
, and 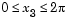 . To evaluate and plot this function:
. To evaluate and plot this function:
x1 =-2:0.2:2;x2 =-2:0.25:2;x3 = -2:0.16:2; [X1,X2,X3] = ndgrid(x1,x2,x3); z = X2.*exp(-X1.^2 -X2.^2 -X3.^2); slice(X2,X1,X3,z,[-1.2 0.8 2],2,[-2 0.2])
 | Comparing Interpolation Methods | Triangulation and Interpolation of Scattered Data |  |