

| Mathematics |   |
Introduction to PDE Problems
pdepe solves systems of PDEs in one spatial variable 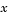 and time
and time 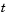 , of the form
, of the form
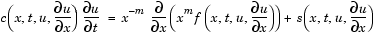
|
(14-4) |
The PDEs hold for 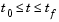 and
and 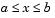 . The interval
. The interval 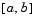 must be finite.
must be finite. 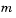 can be 0, 1, or 2, corresponding to slab, cylindrical, or spherical symmetry, respectively. If
can be 0, 1, or 2, corresponding to slab, cylindrical, or spherical symmetry, respectively. If 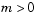 , then
, then 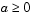 must also hold.
must also hold.
In Equation 14-4, 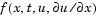 is a flux term and
is a flux term and 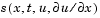 is a source term. The coupling of the partial derivatives with respect to time is restricted to multiplication by a diagonal matrix
is a source term. The coupling of the partial derivatives with respect to time is restricted to multiplication by a diagonal matrix 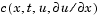 . The diagonal elements of this matrix are either identically zero or positive. An element that is identically zero corresponds to an elliptic equation and otherwise to a parabolic equation. There must be at least one parabolic equation. An element of
. The diagonal elements of this matrix are either identically zero or positive. An element that is identically zero corresponds to an elliptic equation and otherwise to a parabolic equation. There must be at least one parabolic equation. An element of 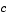 that corresponds to a parabolic equation can vanish at isolated values of
that corresponds to a parabolic equation can vanish at isolated values of 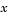 if they are mesh points. Discontinuities in
if they are mesh points. Discontinuities in 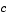 and/or
and/or 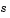 due to material interfaces are permitted provided that a mesh point is placed at each interface.
due to material interfaces are permitted provided that a mesh point is placed at each interface.
At the initial time 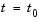 , for all
, for all 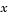 the solution components satisfy initial conditions of the form
the solution components satisfy initial conditions of the form
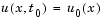
|
(14-5) |
At the boundary 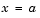 or
or 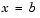 , for all
, for all 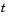 the solution components satisfy a boundary condition of the form
the solution components satisfy a boundary condition of the form
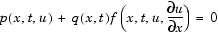
|
(14-6) |
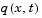 is a diagonal matrix with elements that are either identically zero or never zero. Note that the boundary conditions are expressed in terms of the flux
is a diagonal matrix with elements that are either identically zero or never zero. Note that the boundary conditions are expressed in terms of the flux 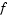 rather than
rather than 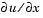 . Also, of the two coefficients, only
. Also, of the two coefficients, only 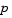 can depend on
can depend on 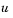 .
.
 | PDE Function Summary | MATLAB Partial Differential Equation Solver |  |