Statistics Toolbox

corr

Correlation coefficients with tests and confidence bounds

Syntax

• R = corr(X)
  R = corr(x,y)
  [R,P] = corr(...)
  [R,P,RLO,RUP] = corr(...)
  [...] = corr(...,'param1',val1,'param2',val2,...)
  

Description

R = corr(X) calculates a matrix R of correlation coefficients for an array X Each row of X is an observation and each column is a variable. NaN (not a number) values in X are treated as missing.

If C is the covariance matrix, C = cov(X), then corr(X) is the matrix whose (i,j)th element is

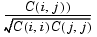
R = corr(x,y) where x and y are column vectors, is the same as R = corr([x y]).

[R,P] = corr(...) also returns P, a matrix of p-values for testing the hypothesis of no correlation. Each p-value is the probability of getting a correlation as large as the observed value by random chance, when the true correlation is zero. If P(i,j) is small, say less than 0.05, then the correlation R(i,j) is significant. See Algorithm for details.

[R,P,RLO,RUP] = corr(...) also returns matrices RLO and RUP, of the same size as R, containing lower and upper bounds for a 95% confidence interval for each coefficient.

[...] = corr(...,'param1',val1,'param2',val2,...) specifies additional parameters and their values. Valid parameters are the following:

'alpha'	A number between 0 and 1 that specifies a confidence level of 100*(1-alpha)%. Default is 0.05 for 95% confidence intervals.
'rows'	'all'	Use all rows.
	'complete'	Use rows with no missing values (default).
	'pairwise'	Compute R(i,j) using rows with no missing values in column i or j.

Examples

• load hogg;              % load sample data 
  [r,p,rlo,rup] = corr([x1 x2 x3 x4 x5],'alpha',0.10); 
  [i,j] = find(p<0.05);   % find significant correlations 
  [i,j]                   % display their indices
  

Algorithm

The p-value is computed by transforming the correlation to create an F statistic having 1 and n-2 degrees of freedom, where n is the number of rows of X. The confidence bounds are based on an asymptotic normal distribution for 0.5*log((1+R)/(1-R)), with an approximate variance equal to 1/(n-3). These bounds are accurate for large samples when X has a multivariate normal distribution.

See Also

corrcoef, cov, nanmean, nanstd, std

cordexch

corrcoef