ugarch (Financial Toolbox)

Univariate GARCH(P,Q) parameter estimation with Gaussian innovations

Syntax

```
[Kappa, Alpha, Beta] = ugarch(U, P, Q)
```

Arguments

U
Single column vector of random disturbances, i.e., the residuals or innovations (_t), of an econometric model representing a mean-zero, discrete-time stochastic process. The innovations time series U is assumed to follow a GARCH(P,Q) process.

P
Non-negative, scalar integer representing a model order of the GARCH process. P is the number of lags of the conditional variance. P can be zero; when P = 0, a GARCH(0,Q) process is actually an ARCH(Q) process.

Q
Positive, scalar integer representing a model order of the GARCH process. Q is the number of lags of the squared innovations.

`U`	Single column vector of random disturbances, i.e., the residuals or innovations (_t), of an econometric model representing a mean-zero, discrete-time stochastic process. The innovations time series `U` is assumed to follow a GARCH(P,Q) process.
`P`	Non-negative, scalar integer representing a model order of the GARCH process. `P` is the number of lags of the conditional variance. `P` can be zero; when `P = 0`, a GARCH(0,Q) process is actually an ARCH(Q) process.
`Q`	Positive, scalar integer representing a model order of the GARCH process. `Q` is the number of lags of the squared innovations.

Description

[Kappa, Alpha, Beta] = ugarch(U, P, Q) computes estimated univariate GARCH(P,Q) parameters with Gaussian innovations.

Kappa is the estimated scalar constant term (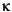) of the GARCH process.

Alpha is a P-by-1 vector of estimated coefficients, where P is the number of lags of the conditional variance included in the GARCH process.

Beta is a Q-by-1 vector of estimated coefficients, where Q is the number of lags of the squared innovations included in the GARCH process.

The time-conditional variance, 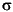_t², of a GARCH(P,Q) process is modeled as

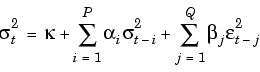
where 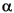represents the argument Alpha, 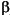represents Beta, and the GARCH(P, Q) coefficients {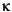, , 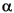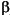} are subject to the following constraints.

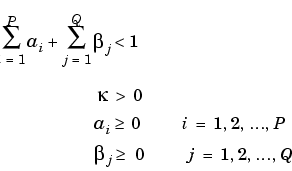
Note that U is a vector of residuals or innovations (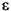_t) of an econometric model, representing a mean-zero, discrete-time stochastic process.

Although 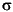_t² is generated using the equation above, 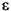_t and 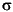_t² are related as

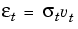
where {v_t} is an independent, identically distributed (i.i.d.) sequence ~ N(0,1).

Note ugarch corresponds generally to the GARCH Toolbox function garchfit. The GARCH Toolbox provides a comprehensive and integrated computing environment for the analysis of volatility in time series. For information, see the GARCH Toolbox User's Guide or the financial products Web page at http://www.mathworks.com/products/finprod/.

Examples

See ugarchsim for an example of a GARCH(P,Q) process.

See Also
ugarchpred, ugarchsim, and the GARCH Toolbox function garchfit

References

James D. Hamilton, Time Series Analysis, Princeton University Press, 1994

tr2bonds ugarchllf