Financial Toolbox

Linear Constraint Equations

While frontcon allows you to enter a fixed set of constraints related to minimum and maximum values for groups and individual assets, you often need to specify a larger and more general set of constraints when finding the optimal risky portfolio. The function portopt addresses this need, by accepting an arbitrary set of constraints as an input matrix.

The auxiliary function portcons can be used to create the matrix of constraints, with each row representing an inequality. These inequalities are of the type A*Wts' <= b, where A is a matrix, b is a vector, and Wts is a row vector of asset allocations. The number of columns of the matrix A, and the length of the vector Wts correspond to the number of assets. The number of rows of the matrix A, and the length of vector b correspond to the number of constraints. This method allows you to specify any number of linear inequalities to the function portopt.

In actuality, portcons is an entry point to a set of functions that generate matrices for specific types of constraints. portcons allows you to specify all the constraints data at once, while the specific portfolio constraint functions allow you to build the constraints incrementally. These constraint functions are pcpval, pcalims, pcglims, and pcgcomp.

Consider an example to help understand how to specify constraints to portopt while bypassing the use of portcons. This example requires specifying the minimum and maximum investment in various groups.

Table 2-5: Maximum and Minimum Group Exposure

Group	Minimum Exposure	Maximum Exposure
North America	0.30	0.75
Europe	0.10	0.55
Latin America	0.20	0.50
Asia	0.50	0.50

Note that the minimum and maximum exposure in Asia is the same. This means that you require a fixed exposure for this group.

Also assume that the portfolio consists of three different funds. The correspondence between funds and groups is shown in Table 2-6.

Table 2-6: Group Membership

Group	Fund 1	Fund 2	Fund 3
North America	X	X
Europe			X
Latin America	X
Asia		X	X

Using the information in these two tables, build a mathematical representation of the constraints represented. Assume that the vector of weights representing the exposure of each asset in a portfolio is called Wts = [W1 W2 W3].

Specifically

1.	W1 + W2		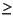0.30
2.	W1 + W2		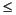0.75
3.	W3		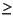0.10
4.	W3		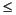0.55
5.	W1		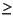0.20
6.	W1		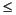0.50
7.	W2 + W3	=	0.50

Since you need to represent the information in the form A*Wts <= b, multiply equations 1, 3 and 5 by -1. Also turn equation 7 into a set of two inequalities: W2 + W3 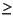0.50 and W2 + W3 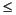0.50 (The intersection of these two inequalities is the equality itself.). Thus

1.	-W1 - W2		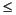-0.30
2.	W1 + W2		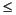0.75
3.	-W3		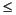-0.10
4.	W3		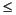0.55
5.	-W1		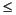-0.20
6.	W1		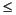0.50
7.	-W2 - W3		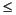-0.50
8.	W2 + W3		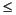0.50

Bringing these equations into matrix notation gives

• A = [-1    -1     0;
        1     1     0;
        0     0    -1;
        0     0     1;
       -1     0     0;
        1     0     0;
        0    -1    -1;
        0     1     1]
  
  b = [-0.30;
        0.75;
       -0.10;
        0.55;
       -0.20;
        0.50;
       -0.50;
        0.50]
  

Build the constraint matrix ConSet by concatenating the matrix A to the vector b.

• ConSet = [A, b] 
  

Portfolio Construction Examples

Specifying Additional Constraints