

| Wavelet Toolbox |   |
Organizing the Wavelet Packets
The set of functions Wj,n = (Wj,n,k(x), 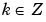 ) is the (j,n) wavelet packet. For positive values of integers j and n, wavelet packets are organized in trees. The tree in Figure 6-40 is created to give a maximum level decomposition equal to 3. For each scale j, the possible values of parameter n are 0, 1, ..., 2j -1.
) is the (j,n) wavelet packet. For positive values of integers j and n, wavelet packets are organized in trees. The tree in Figure 6-40 is created to give a maximum level decomposition equal to 3. For each scale j, the possible values of parameter n are 0, 1, ..., 2j -1.
Figure 6-40: Wavelet Packets Organized in a Tree; Scale j Defines Depth and Frequency n Defines Position in the Tree
The notation Wj,n, where j denotes scale parameter and n the frequency parameter, is consistent with the usual depth-position tree labeling.
It turns out that the library of wavelet packet bases contains the wavelet basis and also several other bases. Let us have a look at some of those bases. More precisely, let V0 denote the space (spanned by the family W0,0) in which the signal to be analyzed lies; then (Wd,1; d 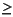 1) is an orthogonal basis of V0.
1) is an orthogonal basis of V0.
For every strictly positive integer D, (WD,0, (Wd,1; 1 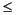 d
d 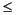 D)) is an orthogonal basis of V0.
D)) is an orthogonal basis of V0.
We also know that the family of functions {(Wj+1,2n),(Wj+1,2n+1)} is an orthogonal basis of the space spanned by Wj,n, which is split into two subspaces: Wj+1,2n spans the first subspace, and Wj+1,2n+1 the second one.
This last property gives a precise interpretation of splitting in the wavelet packet organization tree, because all the developed nodes are of the form shown in the figure below.
Figure 6-41: Wavelet Packet Tree: Split and Merge
It follows that the leaves of every connected binary subtree of the complete tree correspond to an orthogonal basis of the initial space.
For a finite energy signal belonging to V0, any wavelet packet basis will provide exact reconstruction and offer a specific way of coding the signal, using information allocation in frequency scale subbands.
 | Wavelet Packet Atoms | Choosing the Optimal Decomposition |  |