| Statistics Toolbox | |
Poisson Distribution
The following sections provide an overview of the Poisson distribution.
Background of the Poisson Distribution
The Poisson distribution is appropriate for applications that involve counting the number of times a random event occurs in a given amount of time, distance, area, etc. Sample applications that involve Poisson distributions include the number of Geiger counter clicks per second, the number of people walking into a store in an hour, and the number of flaws per 1000 feet of video tape.
The Poisson distribution is a one parameter discrete distribution that takes nonnegative integer values. The parameter,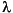 
, is both the mean and the variance of the distribution. Thus, as the size of the numbers in a particular sample of Poisson random numbers gets larger, so does the variability of the numbers.
As Poisson (1837) showed, the Poisson distribution is the limiting case of a binomial distribution where N approaches infinity and p goes to zero while Np = .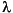
The Poisson and exponential distributions are related. If the number of counts follows the Poisson distribution, then the interval between individual counts follows the exponential distribution.
Definition of the Poisson Distribution
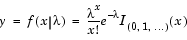
Parameter Estimation for the Poisson Distribution
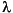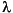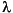The MLE and the MVUE of the Poisson parameter, , is the sample mean. The sum of independent Poisson random variables is also Poisson distributed with the parameter equal to the sum of the individual parameters. The Statistics Toolbox makes use of this fact to calculate confidence intervals on. As gets large the Poisson distribution can be approximated by a normal distribution with µ = 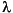and 
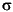2 =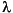. The Statistics Toolbox uses this approximation for calculating confidence intervals for values of 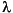greater than 100.
Example and Plot of the Poisson Distribution
The plot shows the probability for each nonnegative integer when 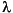= 5.
| | Normal Distribution | Rayleigh Distribution | |
