Statistics Toolbox

Normal Distribution

The following sections provide an overview of the normal distribution.

Background of the Normal Distribution

The normal distribution is a two parameter family of curves. The first parameter, µ, is the mean. The second, 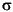, is the standard deviation. The standard normal distribution (written 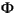(x)) sets µ to 0 and 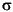to 1.

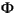(x) is functionally related to the error function, erf.

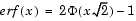
The first use of the normal distribution was as a continuous approximation to the binomial.

The usual justification for using the normal distribution for modeling is the Central Limit Theorem, which states (roughly) that the sum of independent samples from any distribution with finite mean and variance converges to the normal distribution as the sample size goes to infinity.

Definition of the Normal Distribution

The normal pdf is

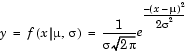
Parameter Estimation for the Normal Distribution

One of the first applications of the normal distribution in data analysis was modeling the height of school children. Suppose we want to estimate the mean, µ, and the variance, 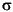², of all the 4th graders in the United States.

We have already introduced MLEs. Another desirable criterion in a statistical estimator is unbiasedness. A statistic is unbiased if the expected value of the statistic is equal to the parameter being estimated. MLEs are not always unbiased. For any data sample, there may be more than one unbiased estimator of the parameters of the parent distribution of the sample. For instance, every sample value is an unbiased estimate of the parameter µ of a normal distribution. The Minimum Variance Unbiased Estimator (MVUE) is the statistic that has the minimum variance of all unbiased estimators of a parameter.

The MVUEs of parameters µ and 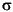² for the normal distribution are the sample average and variance. The sample average is also the MLE for µ. There are two common textbook formulas for the variance.

They are

where

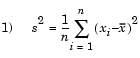
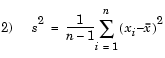
Equation 1 is the maximum likelihood estimator for 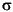², and equation 2 is the MVUE.

The function normfit returns the MVUEs and confidence intervals for µ and 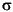². Here is a playful example modeling the "heights" (inches) of a randomly chosen 4th grade class.

• height = normrnd(50,2,30,1);             % Simulate heights.
  [mu,s,muci,sci] = normfit(height)
  mu =
     50.2025
  s =
      1.7946
  muci =
     49.5210
     50.8841
  sci =
      1.4292
      2.4125
  

Example and Plot of the Normal Distribution

The plot shows the "bell" curve of the standard normal pdf, with µ = 0 and 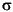 = 1.

Negative Binomial Distribution

Poisson Distribution