

| Statistics Toolbox |   |
Maximum Likelihood Common Factor Analysis
Syntax
lambda = factoran(X,m) [lambda,psi] = factoran(X,m) [lambda,psi,T] = factoran(X,m) [lambda,psi,T,stats] = factoran(X,m) [lambda,psi,T,stats,F] = factoran(X,m) [...] = factoran(...,'param1',value1,'param2',value2,...)
Definition
factoran computes the maximum likelihood estimate (MLE) of the factor loadings matrix 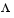 in the Factor Analysis model
in the Factor Analysis model
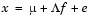
where 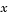 is a vector of observed variables,
is a vector of observed variables, 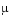 is a constant vector of means,
is a constant vector of means, 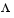 is a constant d-by-m matrix of factor loadings,
is a constant d-by-m matrix of factor loadings, 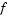 is a vector of independent, standardized common factors, and
is a vector of independent, standardized common factors, and 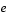 is a vector of independent specific factors.
is a vector of independent specific factors. 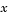 ,
, 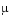 , and
, and 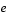 are of length d.
are of length d. 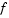 is of length m.
is of length m.
Alternatively, the Factor Analysis model can be specified as
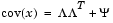
where 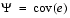 is a d-by-d diagonal matrix of specific variances.
is a d-by-d diagonal matrix of specific variances.
Description
lambda = factoran(X,m)
returns the maximum likelihood estimate, lambda, of the factor loadings matrix, in a common factor analysis model with m common factors. X is an n-by-d matrix where each row is an observation of d variables. The (i,j)th element of the d-by-m matrix lambda is the coefficient, or loading, of the jth factor for the ith variable. By default, the estimated factor loadings are rotated using the 'varimax' option of the 'rotate' parameter.
[lambda,psi] = factoran(X,m)
also returns maximum likelihood estimates of the specific variances as a column vector psi of length d.
[lambda,psi,T] = factoran(X,m)
also returns the m-by-m factor loadings rotation matrix T.
[lambda,psi,T,stats] = factoran(X,m)
also returns a structure stats containing information relating to the null hypothesis, H0, that the number of common factors is m. stats includes the fields:
factoran does not compute the chisq and p fields unless dfe is positive, and all the specific valiance estimates in psi are positive (see Heywood Case below). If X is a covariance matrix, then you must also specify the 'nobs' parameter if you want factoran to compute the chisq and p fields.
[lambda,psi,T,stats,F] = factoran(X,m)
also returns, in F, predictions of the common factors, known as factor scores. F is an n-by-m matrix where each row is a prediction of m common factors. If X is a covariance matrix, factoran cannot compute F. factoran rotates F using the same criterion as for lambda.
[ ... ] = factoran(...,'param1',value1,'param2',value2,...)
enables you to specify optional parameter name/value pairs to control the model fit and the outputs. These are the valid parameters. The most commonly used parameters are listed first.
| Parameter |
Value | |
'xtype' |
The type of input in the matrix X. 'xtype' can be one of: | |
|
'data' |
Raw data (default) |
|
'covariance' |
Positive definite covariance or correlation matrix |
'scores' |
Method for predicting factor scores. 'scores' is ignored if X is not raw data. | |
|
'wls' |
Synonyms for a weighted least squares estimate that treats F as fixed (default) |
|
'regression' |
Synonyms for a minimum mean squared error prediction that is equivalent to a ridge regression |
'start' |
Starting point for the specific variances psi in the maximum likelihood optimization. May be specified as: | |
|
'random' |
Chooses d uniformly distributed values on the interval [0,1]. |
|
'Rsquared' |
Chooses the starting vector as a scale factor times diag(inv(corrcoef(X))) (default). E.g., see Jöreskog [2]. |
|
Performs the given number of maximum likelihood fits, each initialized as with 'random'. factoran returns the fit with the highest likelihood. |
|
|
Performs one maximum likelihood fit for each column of the specified matrix. The ith optimization is initialized with the values from the ith column. The matrix must have d rows. |
|
'rotate' |
Method used to rotate factor loadings and scores. | |
|
'none' |
Performs no rotation |
|
'orthomax' |
Orthogonal rotation that maximizes a criterion based on the variance of the loadings. Use the 'coeffom', 'normalize', 'reltol', and ' |
|
'varimax' |
Special case of the orthomax rotation (default). Use the 'normalize', 'reltol', and ' |
|
'procrustes' |
Performs either an oblique (the default) or an orthogonal rotation to best match a specified target matrix in the least squares sense. Use the 'typeprocr' parameter to choose the type of rotation. Use 'targetprocr' to specify the target matrix. |
|
'promaxpm' |
Performs an oblique procrustes rotation to a target matrix determined by factoran as a function of an orthomax solution.Use the 'powerpm' parameter to specify the exponent for creating the target matrix. Because 'promaxpm' uses 'orthomax' internally, you can also specify the parameters that apply to 'orthomax'. |
|
Function |
Function handle to rotation function of the form where A is a d-by-m matrix of unrotated factor loadings. B is a d-by-m matrix of rotated loadings, and T is the corresponding m-by-m rotation matrix.Use the factoran parameter 'userargs' to pass additional arguments to this rotation function. See Example 4. |
|
Coefficient, often denoted as 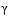 , defining the specific , defining the specific 'orthomax' criterion. Must be between 0 and 1. The value 0 corresponds to quartimax, and 1 corresponds to varimax. Default is 1. | |
'normalize' |
Flag indicating whether the loading matrix should be row-normalized (1) or left unnormalized (0) for 'orthomax' or 'varimax' rotation. Default is 1. | |
'reltol' |
Relative convergence tolerance for 'orthomax' or 'varimax' rotation. Default is sqrt(eps). | |
'maxit' |
Iteration limit for 'orthomax' or 'varimax' rotation. Default is 250. | |
'targetprocr' |
Target factor loading matrix for 'procrustes' rotation. Required for 'procrustes' rotation. No default value. | |
'typeprocr' |
Type of 'procrustes' rotation. Can be 'oblique' (default) or 'orthogonal'. | |
'powerpm' |
Exponent for creating the target matrix in the 'promaxpm' rotation. Must be >= 1. Default is 4. | |
'userargs' |
Denotes the beginning of additional input values for a user-defined rotation function. factoran appends all subsequent values, in order and without processing, to the rotation function argument list, following the unrotated factor loadings matrix A. See Example 4. | |
'nobs' |
If X is a covariance or correlation matrix, indicates the number of observations that were used in its estimation. This allows calculation of significance for the null hypothesis even when the original data are not available. There is no default. 'nobs' is ignored if X is raw data. | |
'delta' |
A lower bound for the specific variances psi during the maximum likelihood optimization. Default is 0.005. | |
'optimopts' |
Structure containing control options for the maximum likelihood optimization. Create this structure with the MATLAB function optimset. factoran uses the following defaults: | |
|
'Display' |
'notify' |
|
'MaxFunEvals' |
100*d |
|
'MaxIter' |
400 |
|
'TolFun' |
1e-8 |
|
'TolX' |
1e-8 |
Remarks
Observed Data Variables. The variables in the observed data matrix X must be linearly independent, i.e., cov(X) must have full rank, for maximum likelihood estimation to succeed. factoran reduces both raw data and a covariance matrix to a correlation matrix before performing the fit.
factoran standardizes the observed data X to zero mean and unit variance before estimating the loadings lambda. This does not affect the model fit, because MLEs in this model are invariant to scale. However, lambda and psi are returned in terms of the standardized variables, i.e., lambda*lambda'+diag(psi) is an estimate of the correlation matrix of the original data X (although not after an oblique rotation). See Examples 1 and 3.
Heywood Case. If elements of psi are equal to the value of the 'delta' parameter (i.e, they are essentially zero), the fit is known as a Heywood case, and interpretation of the resulting estimates is problematic. In particular, there may be multiple local maxima of the likelihood, each with different estimates of the loadings and the specific variances. Heywood cases can indicate overfitting (i.e., m is too large), but can also be the result of underfitting.
Rotation of Factor Loadings and Scores. Unless you explicitly specify no rotation using the 'rotate' parameter, factoran rotates the estimated factor loadings, lambda, and the factor scores, F. The output matrix T is used to rotate the loadings, i.e., lambda = lambda0*T, where lambda0 is the initial (unrotated) MLE of the loadings. T is an orthogonal matrix for orthogonal rotations, and the identity matrix for no rotation. The inverse of T is known as the primary axis rotation matrix, while T itself is related to the reference axis rotation matrix. For orthogonal rotations, the two are identical.
factoran computes factor scores that have been rotated by inv(T'), i.e., F = F0 * inv(T'), where F0 contains the unrotated predictions. The estimated covariance of F is inv(T'*T), which, for orthogonal or no rotation, is the identity matrix. Rotation of factor loadings and scores is an attempt to create a more easily interpretable structure in the loadings matrix after maximum likelihood estimation.
Examples
Example 1. Load the carbig data, and fit the default model with two factors.
load carbig X = [Acceleration Displacement Horsepower MPG Weight]; X = X(all(~isnan(X),2),:); [Lambda,Psi,T,stats,F] = factoran(X,2,'scores','regression') inv(T'*T) % Estimated correlation matrix of F, == eye(2) Lambda*Lambda' + diag(Psi) % Estimated correlation matrix of X Lambda*inv(T) % Unrotate the loadings F*T' % Unrotate the factor scores
Example 2. Although the estimates are the same, the use of a covariance matrix rather than raw data doesn't let you request scores or significance level.
[Lambda,Psi,T] = factoran(cov(X),2,'xtype','cov') [Lambda,Psi,T] = factoran(corrcoef(X),2,'xtype','cov')
Example 3. Use promax rotation.
[Lambda,Psi,T,stats,F] = factoran(X,2,'rotate','promaxpm',... 'powerpm',4) inv(T'*T) % Est'd correlation matrix of F, no longer eye(2) Lambda*inv(T'*T)*Lambda' + diag(Psi) % Est'd correlation % matrix of X
Plot the rotated variables against the oblique axes.
invT = inv(T) Lambda0 = Lambda*invT plot(Lambda0(:,1),Lambda0(:,2), 'ro'); line([-invT(1,1) invT(1,1) NaN -invT(2,1) invT(2,1)], ... [-invT(1,2) invT(1,2) NaN -invT(2,2) invT(2,2)]); text(invT(:,1), invT(:,2),[' I '; ' II']); xlabel('Loadings for unrotated Factor 1') ylabel('Loadings for unrotated Factor 2')
Example 4. Syntax for passing additional arguments to a user-defined rotation function.
See Also
optimset, princomp, procrustes
References
[1] Harman, H.H., Modern Factor Analysis, 3rd Ed., University of Chicago Press, Chicago, 1976.
[2] Jöreskog, K.G., "Some Contributions to Maximum Likelihood Factor Analysis", Psychometrika, Vol.32, pp.443-482, 1967.
[3] Lawley, D.N. and A.E. Maxwell, Factor Analysis as a Statistical Method, 2nd Ed., American Elsevier Pub. Co., New York, 1971.
 | expstat | fcdf |  |