

| Function Reference |   |
Design linear-quadratic (LQ) state-feedback regulator for discrete-time plant
Syntax
Description
[K,S,e] = dlqr(a,b,Q,R,N)
K such that the state-feedback law
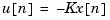
minimizes the quadratic cost function
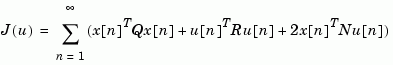
for the discrete-time state-space mode
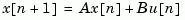
The default value N=0 is assumed when N is omitted.
In addition to the state-feedback gain K, dlqr returns the infinite horizon solution S of the associated discrete-time Riccati equation
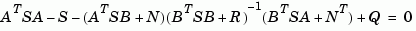
and the closed-loop eigenvalues e = eig(a-b*K). Note that K is derived from S by
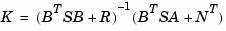
Limitations
The problem data must satisfy:
See Also
dare Solve discrete Riccati equations
lqgreg LQG regulator
lqr State-feedback LQ regulator for continuous plant
lqrd Discrete LQ regulator for continuous plant
lqry State-feedback LQ regulator with output weighting
 | delay2z | dlyap |  |