

| Function Reference |   |
Solve discrete-time algebraic Riccati equations (DARE)
Syntax
[X,L,G,rr] = dare(A,B,Q,R) [X,L,G,rr] = dare(A,B,Q,R,S,E) [X,L,G,report] = dare(A,B,Q,...,'report') [X1,X2,L,report] = dare(A,B,Q,...,'implicit')
Description
[X,L,G,rr] = dare(A,B,Q,R)
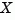 of the discrete-time algebraic Riccati equation
of the discrete-time algebraic Riccati equation
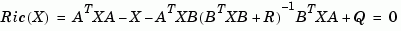
such that the "closed-loop" matrix
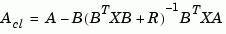
has all its eigenvalues inside the unit disk. The matrix 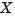 is symmetric and called the stabilizing solution of
is symmetric and called the stabilizing solution of 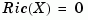 .
. [X,L,G,rr] = dare(A,B,Q,R) also returns:
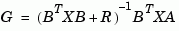
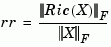
[X,L,G,rr] = dare(A,B,Q,R,S,E)
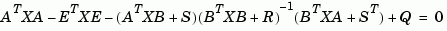
The corresponding gain matrix and closed-loop eigenvalues are
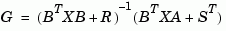
Two additional syntaxes are provided to help develop applications such as 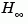 -optimal control design.
-optimal control design.
[X,L,G,report] = dare(A,B,Q,...,'report') turns off the error messages when the solution  fails to exist and returns a failure report instead. The value of
fails to exist and returns a failure report instead. The value of report is:
-1 when the associated symplectic pencil has eigenvalues on or very near the unit circle (failure)
-2 when there is no finite solution, that is, 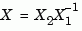 with
with 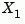 singular (failure)
singular (failure)
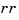 defined above when the solution exists (success)
defined above when the solution exists (success)
Alternatively, [X1,X2,L,report] = dare(A,B,Q,...,'implicit') also turns off error messages but now returns 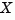 in implicit form as
in implicit form as
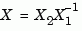
Note that this syntax returns report = 0 when successful.
Algorithm
dare implements the algorithms described in [1]. It uses the QZ algorithm to deflate the extended symplectic pencil and compute its stable invariant subspace.
Limitations
The 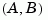 pair must be stabilizable (that is, all eigenvalues of
pair must be stabilizable (that is, all eigenvalues of 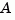 outside the unit disk must be controllable). In addition, the associated symplectic pencil must have no eigenvalue on the unit circle. Sufficient conditions for this to hold are
outside the unit disk must be controllable). In addition, the associated symplectic pencil must have no eigenvalue on the unit circle. Sufficient conditions for this to hold are 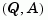 detectable when
detectable when 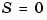 and
and 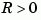 , or
, or
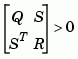
See Also
care Solve continuous-time Riccati equations
dlyap Solve discrete-time Lyapunov equations
References
[1] Arnold, W.F., III and A.J. Laub, "Generalized Eigenproblem Algorithms and Software for Algebraic Riccati Equations," Proc. IEEE, 72 (1984), pp. 1746-1754.
 | damp | dcgain |  |