

| Wavelet Toolbox |   |
Wavelets and Associated Families
In the one-dimensional context, we distinguish the wavelet 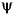 from the associated function
from the associated function 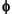 , called the scaling function. Some properties of
, called the scaling function. Some properties of 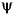 and
and 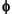 are
are
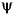 is zero,
is zero,  , and
, and 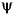 is used to define the details.
is used to define the details.
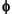 is 1,
is 1, 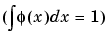 , and
, and 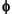 is used to define the approximations.
is used to define the approximations.
The usual two-dimensional wavelets are defined as tensor products of one-dimensional wavelets: 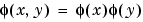 is the scaling function and
is the scaling function and
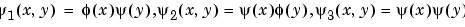 are the three wavelets.
are the three wavelets.
The following figure shows the four functions associated with the two-dimensional coif2 wavelet.
Figure 6-2: Two-Dimensional coif2 Wavelet
To each of these functions, we associate its doubly indexed family, which is used to
 ) (see Figure 6-4,).
) (see Figure 6-4,).
So a wavelet family member has to be thought as a function located at a position b, and having a scale a.
In one-dimensional situations, the family of translated and scaled wavelets associated with 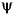 is expressed as follows.
is expressed as follows.
| Translation |
Change of Scale |
Translation and Change of Scale |
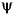 (x-b) (x-b) |
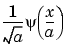 |
|
Figure 6-3: Translated Wavelets
Figure 6-4: Time Scaled One-Dimensional Wavelet
In a two-dimensional context, we have the translation by vector 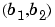 and a change of scale of parameter
and a change of scale of parameter 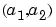 .
.
Translation and change of scale become
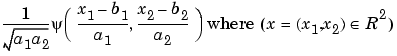
In most cases, we will limit our choice of a and b values by using only the following discrete set (coming back to the one-dimensional context):
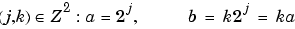
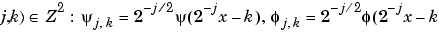
We now have a hierarchical organization similar to the organization of a decomposition; this is represented in the example of Figure 6-5, Wavelets Organization. Let k = 0 and leave the translations aside for the moment. The functions associated with j = 0, 1, 2, 3 for 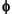 (expressed as
(expressed as 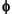 j,0) and with j = 1, 2, 3 for
j,0) and with j = 1, 2, 3 for 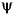 (expressed as
(expressed as 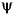 j,0) are displayed in the following figure for the
j,0) are displayed in the following figure for the db3 wavelet.
Figure 6-5: Wavelets Organization
In Figure 6-5, Wavelets Organization, the four-level decomposition is shown, progressing from the top to the bottom. We find 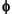 0,0; then 21/2
0,0; then 21/2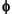 1,0, 21/2
1,0, 21/2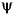 1,0; then 2
1,0; then 2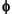 2,0, 2
2,0, 2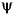 2,0; then 23/2
2,0; then 23/2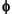 3,0, 23/2
3,0, 23/2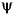 3,0. The wavelet is
3,0. The wavelet is db3.
 | Wavelet Shapes | Wavelet Transforms: Continuous and Discrete |  |