Optimization Toolbox

Unconstrained Minimization Example

Consider the problem of finding a set of values [x₁, x₂] that solves

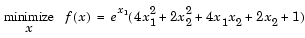
(2-1)

To solve this two-dimensional problem, write an M-file that returns the function value. Then, invoke the unconstrained minimization routine fminunc.

Step 1: Write an M-file objfun.m.

• function f = objfun(x)
  f = exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
  

Step 2: Invoke one of the unconstrained optimization routines.

• x0 = [-1,1];    % Starting guess
  options = optimset('LargeScale','off');
  [x,fval,exitflag,output] = fminunc(@objfun,x0,options);
  

After 40 function evaluations, this produces the solution

• x =
        0.5000   -1.0000
  

The function at the solution x is returned in fval:

• fval =
        1.3030e-10
  

The exitflag tells whether the algorithm converged. An exitflag > 0 means a local minimum was found:

• exitflag =
       1
  

The output structure gives more details about the optimization. For fminunc, it includes the number of iterations in iterations, the number of function evaluations in funcCount, the final step-size in stepsize, a measure of first-order optimality (which in this unconstrained case is the infinity norm of the gradient at the solution) in firstorderopt, and the type of algorithm used in algorithm:

• output = 
         iterations: 7
          funcCount: 40
           stepsize: 1
      firstorderopt: 9.2801e-004
          algorithm: 'medium-scale: Quasi-Newton line search'
  

When more than one local minimum exists, the initial guess for the vector [x₁, x₂] affects both the number of function evaluations and the value of the solution point. In the preceding example, x0 is initialized to [-1,1].

The variable options can be passed to fminunc to change characteristics of the optimization algorithm, as in

• x = fminunc(@objfun,x0,options);
  

options is a structure that contains values for termination tolerances and algorithm choices. An options structure can be created using the optimset function:

• options = optimset('LargeScale','off');
  

In this example, we have turned off the default selection of the large-scale algorithm and so the medium-scale algorithm is used. Other options include controlling the amount of command line display during the optimization iteration, the tolerances for the termination criteria, whether a user-supplied gradient or Jacobian is to be used, and the maximum number of iterations or function evaluations. See optimset, the individual optimization functions, and Table 5, Optimization Parameters, for more options and information.

Examples that Use Standard Algorithms

Nonlinear Inequality Constrained Example