fzero (Optimization Toolbox)

Zero of a continuous function of one variable

Syntax

x = fzero(fun,x0)
x = fzero(fun,x0,options)
x = fzero(fun,x0,options,P1,P2,...)
[x,fval] = fzero(...)
[x,fval,exitflag] = fzero(...)
[x,fval,exitflag,output] = fzero(...)

Description

x = fzero(fun,x0) tries to find a zero of fun near x0, if x0 is a scalar. The value x returned by fzero is near a point where fun changes sign, or NaN if the search fails. In this case, the search terminates when the search interval is expanded until an Inf, NaN, or complex value is found.

If x0 is a vector of length two, fzero assumes x0 is an interval where the sign of fun(x0(1)) differs from the sign of fun(x0(2)). An error occurs if this is not true. Calling fzero with such an interval guarantees fzero returns a value near a point where fun changes sign.

Note Calling fzero with an interval (x0 with two elements) is often faster than calling it with a scalar x0.

x = fzero(fun,x0,options) minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters.

x = fzero(fun,x0,options,P1,P2,...) provides for additional arguments, P1, P2, etc., which are passed to the objective function, fun. Use options = [] as a placeholder if no options are set.

[x,fval] = fzero(...) returns the value of the objective function fun at the solution x.

[x,fval,exitflag] = fzero(...) returns a value exitflag that describes the exit condition.

[x,fval,exitflag,output] = fzero(...) returns a structure output that contains information about the optimization.

Note For the purposes of this command, zeros are considered to be points where the function actually crosses, not just touches, the x-axis.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to fzero. This section provides function-specific details for fun and options:

fun
The function whose zero is to be computed. fun is a function that accepts a vector x and returns a scalar f, the objective function evaluated at x. The function fun can be specified as a function handle.
x = fzero(@myfun,x0)
where myfun is a MATLAB function such as
function f = myfun(x) f = ... % Compute function value at x
fun can also be an inline object.
x = fzero(inline('sin(x*x)'),x0);

options
Optimization parameter options. You can set or change the values of these parameters using the optimset function. fzero uses these options structure fields:

Display
Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' displays just the final output; 'notify' (default) displays output only if the function does not converge.

TolX
Termination tolerance on x.

`fun`	The function whose zero is to be computed. `fun` is a function that accepts a vector `x` and returns a scalar `f`, the objective function evaluated at `x`. The function `fun` can be specified as a function handle. x = fzero(@myfun,x0) where `myfun` is a MATLAB function such as function f = myfun(x) f = ... % Compute function value at x `fun` can also be an inline object. x = fzero(inline('sin(x*x)'),x0);
`options`	Optimization parameter options. You can set or change the values of these parameters using the `optimset` function. `fzero` uses these `options` structure fields:
	`Display`	Level of display. `'off'` displays no output; `'iter'` displays output at each iteration; `'final'` displays just the final output; `'notify'` (default) displays output only if the function does not converge.
	`TolX`	Termination tolerance on `x`.

Output Arguments

Function Arguments contains general descriptions of arguments returned by fzero. This section provides function-specific details for exitflag and output:

exitflag
Describes the exit condition:

> 0
Indicates that fzero found a zero x.

< 0
No interval was found with a sign change, or a NaN or Inf function value was encountered during the search for an interval containing a sign change, or a complex function value was encountered during the search for an interval containing a sign change.

output
Structure containing information about the optimization. The fields of the structure are:

iterations
Number of iterations taken (for fzero, this is the same as the number of function evaluations).

funcCount
Number of function evaluations.

algorithm
Algorithm used.

`exitflag`	Describes the exit condition:
	`> 0`	Indicates that `fzero` found a zero `x`.
	`< 0`	No interval was found with a sign change, or a `NaN` or `Inf` function value was encountered during the search for an interval containing a sign change, or a complex function value was encountered during the search for an interval containing a sign change.
`output`	Structure containing information about the optimization. The fields of the structure are:
	`iterations`	Number of iterations taken (for `fzero`, this is the same as the number of function evaluations).
	`funcCount`	Number of function evaluations.
	`algorithm`	Algorithm used.

Examples

Calculate 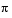by finding the zero of the sine function near 3.

```
x = fzero(@sin,3)
x =
    3.1416
```

To find the zero of cosine between 1 and 2,

x = fzero(@cos,[1 2])
x =
     1.5708

Note that cos(1) and cos(2) differ in sign.

To find a zero of the function

write an M-file called f.m.

```
function y = f(x)
y = x.^3-2*x-5;
```

To find the zero near 2

```
z = fzero(@f,2)
z =
    2.0946
```

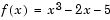
Since this function is a polynomial, the statement roots([1 0 -2 -5]) finds the same real zero, and a complex conjugate pair of zeros.

    2.0946
   -1.0473 + 1.1359i
   -1.0473 - 1.1359i

Algorithm

The fzero command is an M-file. The algorithm, which was originated by T. Dekker, uses a combination of bisection, secant, and inverse quadratic interpolation methods. An Algol 60 version, with some improvements, is given in [1]. A Fortran version, upon which the fzero M-file is based, is in [2].

Limitations

The fzero command finds a point where the function changes sign. If the function is continuous, this is also a point where the function has a value near zero. If the function is not continuous, fzero may return values that are discontinuous points instead of zeros. For example, fzero(@tan,1) returns 1.5708, a discontinuous point in tan.

Furthermore, the fzero command defines a zero as a point where the function crosses the x-axis. Points where the function touches, but does not cross, the x-axis are not valid zeros. For example, y = x.^2 is a parabola that touches the x-axis at 0. Since the function never crosses the x-axis, however, no zero is found. For functions with no valid zeros, fzero executes until Inf, NaN, or a complex value is detected.

See Also

@ (function_handle), \, fminbnd, fsolve, inline, optimset, roots

References

[1] Brent, R., Algorithms for Minimization Without Derivatives, Prentice-Hall, 1973.

[2] Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.

fsolve fzmult