| System Identification Toolbox | |
The Basic Algorithm
A typical recursive identification algorithm is
|
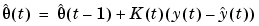
(3-55) |
Here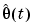 
is the parameter estimate at time t, and 
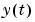is the observed output at time t. Moreover, 
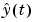is a prediction of the value 
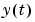based on observations up to time 
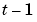and also based on the current model (and possibly also earlier ones) at time 
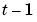. The gain 
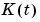determines in what way the current prediction error 
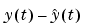affects the update of the parameter estimate. It is typically chosen as
|
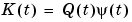
(3-56) |
where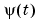 
is (an approximation of) the gradient with respect to 
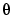of 
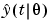. The latter symbol is the prediction of 
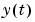according the model described by 
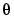. Note that model structures like AR and ARX that correspond to linear regressions can be written as
|
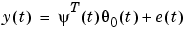
(3-57) |
where the regression vector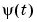 
contains old values of observed inputs and outputs, and 
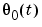represents the true description of the system. Moreover, 
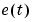is the noise source (the innovations). Compare with (3-14). The natural prediction is 
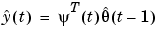and its gradient with respect to 
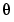becomes exactly 
.
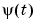For models that cannot be written as linear regressions, you cannot recursively compute the exact prediction and its gradient for the current estimate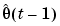 
. Then approximations 
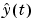and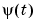 
must be used instead. Section 11.4 in Ljung (1999) describes suitable ways of computing such approximations for general model structures.
The matrix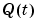 
that affects both the adaptation gain and the direction in which the updates are made, can be chosen in several different ways. This is discussed in the following.
| | Recursive Parameter Estimation | Choosing an Adaptation Mechanism and Gain | |