Statistics Toolbox

ttest2

Hypothesis testing for the difference in means of two samples

Syntax

• h = ttest2(x,y)
  [h,significance,ci] = ttest2(x,y,alpha)
  [h,significance,ci,stats] = ttest2(x,y,alpha)
  [...] = ttest2(x,y,alpha,tail)
  

Description

h = ttest2(x,y) performs a t-test to determine whether two samples from a normal distribution (in x and y) could have the same mean when the standard deviations are unknown but assumed equal.

The result, h, is 1 if you can reject the null hypothesis at the 0.05 significance level alpha and 0 otherwise.

The significance is the p-value associated with the T-statistic

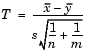
where s is the pooled sample standard deviation and n and m are the numbers of observations in the x and y samples. significance is the probability that the observed value of T could be as large or larger by chance under the null hypothesis that the mean of x is equal to the mean of y.

ci is a 95% confidence interval for the true difference in means.

[h,significance,ci] = ttest2(x,y,alpha) gives control of the significance level alpha. For example if alpha = 0.01, and the result, h, is 1, you can reject the null hypothesis at the significance level 0.01. ci in this case is a 100(1-alpha)% confidence interval for the true difference in means.

[h,significance,ci,stats] = ttest2(x,y,alpha) returns a structure stats with two elments, tstat and df. The tstat element is the value of the t statistic, and df is its degree of freedom.

[...] = ttest2(x,y,alpha,tail) allows specification of one- or two-tailed tests, where tail is a flag that specifies one of three alternative hypotheses:

• tail =  0 specifies the alternative 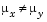(default)
• tail =  1 specifies the alternative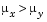
• tail = -1 specifies the alternative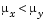

Examples

This example generates 100 normal random numbers with theoretical mean 0 and standard deviation 1. We then generate 100 more normal random numbers with theoretical mean 1/2 and standard deviation 1. The observed means and standard deviations are different from their theoretical values, of course. We test the hypothesis that there is no true difference between the two means. Notice that the true difference is only one half of the standard deviation of the individual observations, so we are trying to detect a signal that is only one half the size of the inherent noise in the process.

• x = normrnd(0,1,100,1);
  y = normrnd(0.5,1,100,1);
  [h,significance,ci] = ttest2(x,y)
  h =
      1
  significance =
      0.0017
  ci =
     -0.7352   -0.1720
  

The result h = 1 means that we can reject the null hypothesis. The significance is 0.0017, which means that by chance we would have observed values of t more extreme than the one in this example in only 17 of 10,000 similar experiments! A 95% confidence interval on the mean is [-0.7352 -0.1720], which includes the theoretical (and hypothesized) difference of -0.5.

ttest

unidcdf