regstats (Statistics Toolbox)

Regression diagnostics for linear models

Syntax

regstats(responses,DATA,'model')'
stats = regstats(responses,DATA,'model','whichstats')

Description

regstats(responses,data,'model') fits a multiple regression of the measurements in the vector, responses, on the values in the matrix, DATA. The function creates a UI that displays a group of checkboxes that save diagnostic statistics to the base workspace using specified variable names. 'model' controls the order of the regression model. By default, regstats uses a linear additive model with a constant term.

'model' can be one of the following strings

'linear'
Includes constant and linear terms (default).

'interaction'
Includes constant, linear, and cross product terms.

'quadratic'
Includes interactions and squared terms.

'purequadratic'
Includes constant, linear, and squared terms.

`'linear'`	Includes constant and linear terms (default).
`'interaction'`	Includes constant, linear, and cross product terms.
`'quadratic'`	Includes interactions and squared terms.
`'purequadratic'`	Includes constant, linear, and squared terms.

The order of the coefficients is the order defined by the x2fx function.

stats = regstats(responses,DATA,model,whichstats) creates an output structure stats containing the statistics listed in 'whichstats'. 'whichstats' can be a single name such as 'leverage' or a cell array of names such as {'leverage' 'standres' 'studres'}. Valid names are:

'Q'
Q from the QR Decomposition of X

'R'
R from the QR Decomposition of X

'beta'
Regression Coefficients

'covb'
Covariance of Regression Coefficients

'yhat'
Fitted Values of the Response Data

'r'
Residuals

'mse'
Mean Squared Error

'leverage'
Leverage

'hatmat'
Hat (Projection) Matrix

's2_i'
Delete-1 Variance

'beta_i'
Delete-1 Coefficients

'standres'
Standardized Residuals

'studres'
Studentized Residuals

'dfbetas'
Scaled Change in Regression Coefficients

'dffit'
Change in Fitted Values

'dffits'
Scaled Change in Fitted Values

'covratio'
Change in Covariance

'cookd'
Cook's Distance

'all'
Create all of the above statistics

`'Q'`	Q from the QR Decomposition of X
`'R'`	R from the QR Decomposition of X
`'beta'`	Regression Coefficients
`'covb'`	Covariance of Regression Coefficients
`'yhat'`	Fitted Values of the Response Data
`'r'`	Residuals
`'mse'`	Mean Squared Error
`'leverage'`	Leverage
`'hatmat'`	Hat (Projection) Matrix
`'s2_i'`	Delete-1 Variance
`'beta_i'`	Delete-1 Coefficients
`'standres'`	Standardized Residuals
`'studres'`	Studentized Residuals
`'dfbetas'`	Scaled Change in Regression Coefficients
`'dffit'`	Change in Fitted Values
`'dffits'`	Scaled Change in Fitted Values
`'covratio'`	Change in Covariance
`'cookd'`	Cook's Distance
`'all'`	Create all of the above statistics

For more detail press the Help button in the regstats window. This provides formulae and interpretations for each of these regression diagnostics.

Algorithm

The usual regression model is y = X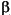 + 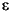, where:

y is an n-by-1 vector of responses
X is an n-by-p matrix of predictors
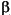is an p-by-1 vector of parameters
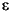is an n-by-1 vector of random disturbances

Let X = Q*R where Q and R come from a QR Decomposition of X. Q is orthogonal and R is triangular. Both of these matrices are useful for calculating many regression diagnostics (Goodall 1993).

The standard textbook equation for the least squares estimator of 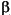is

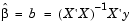
However, this definition has poor numeric properties. Particularly dubious is the computation of 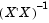, which is both expensive and imprecise.

Numerically stable MATLAB code for 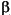is

```
b = R\(Q'*y);
```

See Also
leverage, stepwise, regress

Reference

[1] Belsley, D.A., E. Kuh, and R.E. Welsch , Regression Diagnostics, New York: Wiley, 1980.

[2] Cook, R.D., and S. Weisberg, Residuals and Influence in Regression, New York: Wiley, 1982.

[3] Goodall, C. R., "Computation using the QR decomposition," Statistical Computing (C. R. Rao, ed.), Handbook in Statistics, Volume 9. Amsterdam, NL Elsevier/North-Holland, 1993.

regress ridge