Statistics Toolbox

Probability Density Function (pdf)

The probability density function (pdf) has a different meaning depending on whether the distribution is discrete or continuous.

For discrete distributions, the pdf is the probability of observing a particular outcome. In our videotape example, the probability that there is exactly one defect in a given hundred feet of tape is the value of the pdf at 1.

Unlike discrete distributions, the pdf of a continuous distribution at a value is not the probability of observing that value. For continuous distributions the probability of observing any particular value is zero. To get probabilities you must integrate the pdf over an interval of interest. For example the probability of the thickness of a videotape being between one and two millimeters is the integral of the appropriate pdf from one to two.

A pdf has two theoretical properties:

• The pdf is zero or positive for every possible outcome.
• The integral of a pdf over its entire range of values is one.

A pdf is not a single function. Rather a pdf is a family of functions characterized by one or more parameters. Once you choose (or estimate) the parameters of a pdf, you have uniquely specified the function.

The pdf function call has the same general format for every distribution in the Statistics Toolbox. The following commands illustrate how to call the pdf for the normal distribution.

• x = [-3:0.1:3];
  f = normpdf(x,0,1);
  

The variable f contains the density of the normal pdf with parameters µ=0 and 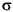=1 at the values in x. The first input argument of every pdf is the set of values for which you want to evaluate the density. Other arguments contain as many parameters as are necessary to define the distribution uniquely. The normal distribution requires two parameters; a location parameter (the mean, µ) and a scale parameter (the standard deviation, ).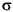

Overview of the Functions

Cumulative Distribution Function (cdf)