Statistics Toolbox

friedman

Friedman's nonparametric two-way Analysis of Variance (ANOVA)

Syntax

• p = friedman(X,reps) 
  p = friedman(X,reps,'displayopt') 
  [p,table] = friedman(...)
  [p,table,stats] = friedman(...)
  

Description

p = friedman(X,reps) performs the nonparametric Friedman's test to compare the means of the columns of X. Friedman's test is similar to classical two-way ANOVA, but it tests only for column effects after adjusting for possible row effects. It does not test for row effects or interaction effects. Friedman's test is appropriate when columns represent treatments that are under study, and rows represent nuisance effects (blocks) that need to be taken into account but are not of any interest.

The different columns represent changes in factor A. The different rows represent changes in the blocking factor B. If there is more than one observation for each combination of factors, input reps indicates the number of replicates in each "cell," which must be constant.

The matrix below illustrates the format for a set-up where column factor A has three levels, row factor B has two levels, and there are two replicates (reps=2). The subscripts indicate row, column, and replicate, respectively.

Friedman's test assumes a model of the form

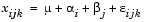
where 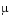is an overall location parameter, 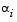represents the column effect, 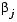represents the row effect, and 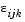represents the error. This test ranks the data within each level of B, and tests for a difference across levels of A. The p that friedman returns is the p-value for the null hypothesis that 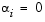. If the p-value is near zero, this casts doubt on the null hypothesis. A sufficiently small p-value suggests that at least one column-sample mean is significantly different than the other column-sample means; i.e., there is a main effect due to factor A. The choice of a limit for the p-value to determine whether a result is "statistically significant" is left to the researcher. It is common to declare a result significant if the p-value is less than 0.05 or 0.01.

friedman also displays a figure showing an ANOVA table, which divides the variability of the ranks into two or three parts:

• The variability due to the differences among the column means
• The variability due to the interaction between rows and columns (if reps is greater than its default value of 1)
• The remaining variability not explained by any systematic source

The ANOVA table has six columns:

• The first shows the source of the variability.
• The second shows the Sum of Squares (SS) due to each source.
• The third shows the degrees of freedom (df) associated with each source.
• The fourth shows the Mean Squares (MS), which is the ratio SS/df.
• The fifth shows Friedman's chi-square statistic.
• The sixth shows the p-value for the chi-square statistic.

p = friedman(X,reps,'displayopt') enables the ANOVA table display when 'displayopt' is 'on' (default) and suppresses the display when 'displayopt' is 'off'.

[p,table] = friedman(...) returns the ANOVA table (including column and row labels) in cell array table. (You can copy a text version of the ANOVA table to the clipboard by selecting Copy Text from the Edit menu.

[p,table,stats] = friedman(...) returns a stats structure that you can use to perform a follow-up multiple comparison test. The friedman test evaluates the hypothesis that the column effects are all the same against the alternative that they are not all the same. Sometimes it is preferable to perform a test to determine which pairs of column effects are significantly different, and which are not. You can use the multcompare function to perform such tests by supplying the stats structure as input.

Examples

Let's repeat the example from the anova2 function, this time applying Friedman's test. Recall that the data below come from a study of popcorn brands and popper type (Hogg 1987). The columns of the matrix popcorn are brands (Gourmet, National, and Generic). The rows are popper type (Oil and Air). The study popped a batch of each brand three times with each popper. The values are the yield in cups of popped popcorn.

• load popcorn
  popcorn
  popcorn =
      5.5000    4.5000    3.5000
      5.5000    4.5000    4.0000
      6.0000    4.0000    3.0000
      6.5000    5.0000    4.0000
      7.0000    5.5000    5.0000
      7.0000    5.0000    4.5000
  p = friedman(popcorn,3)
  p =
      0.0010
  
  
  

The small p-value of 0.001 indicates the popcorn brand affects the yield of popcorn. This is consistent with the results from anova2.

We could also test popper type by permuting the popcorn array as described on Friedman's Test and repeating the test.

References

[1]  Hogg, R. V. and J. Ledolter. Engineering Statistics. MacMillan Publishing Company, 1987.

Hollander, M. and D. A. Wolfe. Nonparametric Statistical Methods. Wiley, 1973.

See Also
anova2, multcompare

fracfact

frnd