

| Function Reference |   |
Syntax
Description
modred
reduces the order of a continuous or discrete state-space model sys. This function is usually used in conjunction with balreal. Two order reduction techniques are available:
rsys = modred(sys,elim) or rsys = modred(sys,elim,'mdc') produces a reduced-order model rsys with matching DC gain (or equivalently, matching steady state in the step response). The index vector elim specifies the states to be eliminated. The resulting model rsys has length(elim) fewer states. This technique consists of setting the derivative of the eliminated states to zero and solving for the remaining states.
rsys = modred(sys,elim,'del')simply deletes the states specified by elim. While this method does not guarantee matching DC gains, it tends to produce better approximations in the frequency domain (see example below).
If the state-space model sys has been balanced with balreal and the grammians have 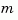 small diagonal entries, you can reduce the model order by eliminating the last
small diagonal entries, you can reduce the model order by eliminating the last 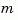 states with
states with modred.
Example
Consider the continuous fourth-order model
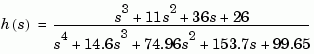
To reduce its order, first compute a balanced state-space realization with balreal by typing
The last three diagonal entries of the balanced grammians are small, so eliminate the last three states with modred using both matched DC gain and direct deletion methods.
Both hmdc and hdel are first-order models. Compare their Bode responses against that of the original model 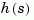 .
.
The reduced-order model hdel is clearly a better frequency-domain approximation of 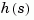 . Now compare the step responses.
. Now compare the step responses.
While hdel accurately reflects the transient behavior, only hmdc gives the true steady-state response.
Algorithm
The algorithm for the matched DC gain method is as follows. For continuous-time models

the state vector is partitioned into 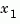 , to be kept, and
, to be kept, and 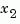 , to be eliminated.
, to be eliminated.
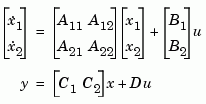
Next, the derivative of 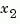 is set to zero and the resulting equation is solved for
is set to zero and the resulting equation is solved for 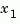 . The reduced-order model is given by
. The reduced-order model is given by
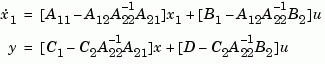
The discrete-time case is treated similarly by setting
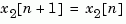
Limitations
With the matched DC gain method, 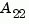 must be invertible in continuous time, and
must be invertible in continuous time, and 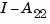 must be invertible in discrete time.
must be invertible in discrete time.
See Also
balreal
minreal
 | minreal | ndims |  |