

| Design Case Studies |   |
Discrete Kalman Filter
The equations of the steady-state Kalman filter for this problem are given as follows.
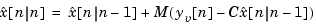
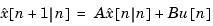
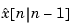 is the estimate of
is the estimate of 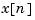 given past measurements up to
given past measurements up to 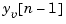
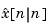 is the updated estimate based on the last measurement
is the updated estimate based on the last measurement 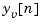
Given the current estimate 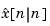 , the time update predicts the state value at the next sample
, the time update predicts the state value at the next sample 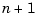 (one-step-ahead predictor). The measurement update then adjusts this prediction based on the new measurement
(one-step-ahead predictor). The measurement update then adjusts this prediction based on the new measurement 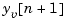 . The correction term is a function of the innovation, that is, the discrepancy.
. The correction term is a function of the innovation, that is, the discrepancy.
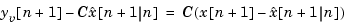
between the measured and predicted values of 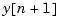 . The innovation gain
. The innovation gain 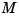 is chosen to minimize the steady-state covariance of the estimation error given the noise covariances
is chosen to minimize the steady-state covariance of the estimation error given the noise covariances

You can combine the time and measurement update equations into one state-space model (the Kalman filter).
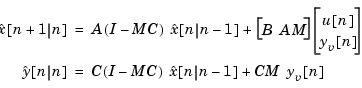
This filter generates an optimal estimate 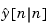 of
of 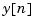 . Note that the filter state is
. Note that the filter state is 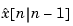 .
.
 | Kalman Filtering | Steady-State Design |  |