

| Wavelet Toolbox |   |
Wavelet Shapes
One-dimensional analysis is based on one scaling function 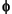 and one wavelet
and one wavelet 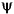 . Two-dimensional analysis (on a square or rectangular grid) is based on one scaling function
. Two-dimensional analysis (on a square or rectangular grid) is based on one scaling function  and three wavelets.
and three wavelets.
THe following figure shows 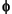 and
and 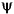 for each wavelet, except the Morlet wavelet and the Mexican hat, for which
for each wavelet, except the Morlet wavelet and the Mexican hat, for which 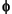 does not exist. All the functions decay quickly to zero. The Haar wavelet is the only noncontinuous function with three points of discontinuity (0, 0.5, 1). The
does not exist. All the functions decay quickly to zero. The Haar wavelet is the only noncontinuous function with three points of discontinuity (0, 0.5, 1). The 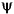 functions oscillate more than associated
functions oscillate more than associated 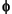 functions.
functions. coif2 exhibits some angular points; db6 and sym6 are quite smooth. The Morlet and Mexican hat wavelets are symmetrical.
Figure 6-1 Various One-Dimensional Wavelets
 | Finer and Coarser Resolutions | Wavelets and Associated Families |  |