ztest (Statistics Toolbox)

Hypothesis testing for the mean of one sample with known variance

Syntax

h = ztest(x,m,sigma)
h = ztest(x,m,sigma,alpha)
[h,sig,ci,zval] = ztest(x,m,sigma,alpha,tail)

Description

h = ztest(x,m,sigma) performs a Z test at significance level 0.05 to determine whether a sample x from a normal distribution with standard deviation sigma could have mean m.

h = ztest(x,m,sigma,alpha) gives control of the significance level alpha. For example, if alpha = 0.01 and the result is h = 1, you can reject the null hypothesis at the significance level 0.01. If h = 0, you cannot reject the null hypothesis at the alpha level of significance.

[h,sig,ci] = ztest(x,m,sigma,alpha,tail) allows specification of one- or two-tailed tests, where tail is a flag that specifies one of three alternative hypotheses:

tail = 0 specifies the alternative 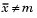(default)
tail = 1 specifies the alternative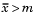
tail = -1 specifies the alternative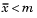

zval is the value of the Z statistic

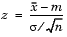
where 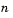is the number of observations in the sample.

sig is the probability that the observed value of Z could be as large or larger by chance under the null hypothesis that the mean of x is equal to m.

ci is a 1-alpha confidence interval for the true mean.

Example

This example generates 100 normal random numbers with theoretical mean zero and standard deviation one. The observed mean and standard deviation are different from their theoretical values, of course. We test the hypothesis that there is no true difference.

x = normrnd(0,1,100,1);
m = mean(x)
m =
    0.0727
[h,sig,ci] = ztest(x,0,1)
h =
     0
sig =
    0.4669
ci =
   -0.1232    0.2687

The result, h = 0, means that we cannot reject the null hypothesis. The significance level is 0.4669, which means that by chance we would have observed values of Z more extreme than the one in this example in 47 of 100 similar experiments. A 95% confidence interval on the mean is [-0.1232 0.2687], which includes the theoretical (and hypothesized) mean of zero.

zscore Selected Bibliography