Statistics Toolbox

var

Variance of a sample

Syntax

• y = var(X)
  y = var(X,1)
  y = var(X,w)
  

Description

y = var(X) computes the variance of the data in X. For vectors, var(x) is the variance of the elements in x. For matrices, var(X) is a row vector containing the variance of each column of X.

y = var(x) normalizes by n-1 where n is the sequence length. For normally distributed data, this makes var(x) the minimum variance unbiased estimator MVUE of 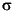²(the second parameter).

y = var(x,1) normalizes by n and yields the second moment of the sample data about its mean (moment of inertia).

y = var(X,w) computes the variance using the vector of positive weights w. The number of elements in w must equal the number of rows in the matrix X. For vector x, w and x must match in length.

var supports both common definitions of variance. Let SS be the sum of
the squared deviations of the elements of a vector x from their mean. Then, var(x) = SS/(n-1) is the MVUE, and var(x,1) = SS/n is the maximum likelihood estimator (MLE) of 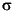².

Examples

• x = [-1 1];
  w = [1 3];
  v1 = var(x)
  v1 =
       2
  v2 = var(x,1)
  v2 =
       1
  v3 = var(x,w)
  v3 =
      0.7500
  

See Also
cov, std

unifstat

weibcdf