Statistics Toolbox

Lognormal Distribution

The following sections provide an overview of the lognormal distribution.

Background of the Lognormal Distribution

The normal and lognormal distributions are closely related. If X is distributed lognormal with parameters µ and 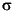², then lnX is distributed normal with parameters µ and 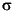².

The lognormal distribution is applicable when the quantity of interest must be positive, since lnX exists only when the random variable X is positive. Economists often model the distribution of income using a lognormal distribution.

Definition of the Lognormal Distribution

The lognormal pdf is

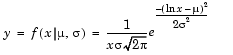
Example and Plot of the Lognormal Distribution

Suppose the income of a family of four in the United States follows a lognormal distribution with µ = log(20,000) and 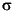² = 1.0. Plot the income density.

• x = (10:1000:125010)';
  y = lognpdf(x,log(20000),1.0);
  plot(x,y)
  set(gca,'xtick',[0 30000 60000 90000 120000])
  set(gca,'xticklabel',str2mat('0','$30,000','$60,000',...
                               '$90,000','$120,000'))
  
  
  

Hypergeometric Distribution

Negative Binomial Distribution