Statistics Toolbox

Factor Analysis

Multivariate data often includes a large number of measured variables, and sometimes those variables "overlap" in the sense that groups of them may be dependent. For example, in a decathalon, each athlete competes in 10 events, but several of them can be thought of as "speed" events, while others can be thought of as "strength" events, etc. Thus, you can think of a competitor's 10 event scores as largely dependent on a smaller set of 3 or 4 types of athletic ability.

Factor Analysis is a way to fit a model to multivariate data to estimate just this sort of interdependence. In the Factor Analysis model, the measured variables depend on a smaller number of unobserved (latent) factors. Because each factor may affect several variables in common, they are known as "common factors". Each variable is assumed to be dependent on a linear combination of the common factors, and the coefficients are known as loadings. Each measured variable also includes a component due to independent random variability, known as "specific variance" because it is specific to one variable.

Specifically, Factor Analysis assumes that the covariance matrix of your data is of the form

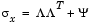
where 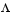is the matrix of loadings, and the elements of the diagonal matrix 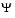are the specific variances. The function factoran fits the Factor Analysis model using maximum likelihood.

This section includes these topics:

• Example: Finding Common Factors Affecting Stock Prices
• Factor Rotation
• Predicting Factor Scores
• Comparison of Factor Analysis and Principal Components Analysis

Hotelling's T2 (Fourth Output)

Example: Finding Common Factors Affecting Stock Prices