Statistics Toolbox

Example: Two-Way ANOVA

The purpose of the example is to determine the effect of car model and factory on the mileage rating of cars.

• load mileage
  mileage
  mileage =
     33.3000   34.5000   37.4000
     33.4000   34.8000   36.8000
     32.9000   33.8000   37.6000
     32.6000   33.4000   36.6000
     32.5000   33.7000   37.0000
     33.0000   33.9000   36.7000
  cars = 3;
  [p,tbl,stats] = anova2(mileage,cars);
  p
  p =
      0.0000    0.0039    0.8411
  

There are three models of cars (columns) and two factories (rows). The reason there are six rows in mileage instead of two is that each factory provides three cars of each model for the study. The data from the first factory is in the first three rows, and the data from the second factory is in the last three rows.

The standard ANOVA table has columns for the sums of squares, degrees-of-freedom, mean squares (SS/df), F statistics, and p-values.

You can use the F statistics to do hypotheses tests to find out if the mileage is the same across models, factories, and model-factory pairs (after adjusting for the additive effects). anova2 returns the p-value from these tests.

The p-value for the model effect is zero to four decimal places. This is a strong indication that the mileage varies from one model to another. An F statistic as extreme as the observed F would occur by chance less than once in 10,000 times if the gas mileage were truly equal from model to model. If you used the multcompare function to perform a multiple comparison test, you would find that each pair of the three models is significantly different.

The p-value for the factory effect is 0.0039, which is also highly significant. This indicates that one factory is out-performing the other in the gas mileage of the cars it produces. The observed p-value indicates that an F statistic as extreme as the observed F would occur by chance about four out of 1000 times if the gas mileage were truly equal from factory to factory.

There does not appear to be any interaction between factories and models. The p-value, 0.8411, means that the observed result is quite likely (84 out 100 times) given that there is no interaction.

The p-values returned by anova2 depend on assumptions about the random disturbances 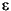_ijk in the model equation. For the p-values to be correct these disturbances need to be independent, normally distributed, and have constant variance. See Robust and Nonparametric Methods for nonparametric methods that do not require a normal distribution.

In addition, anova2 requires that data be balanced, which in this case means there must be the same number of cars for each combination of model and factory. The next section discusses a function that supports unbalanced data with any number of predictors.

Two-Way Analysis of Variance (ANOVA)

N-Way Analysis of Variance