kstest (Statistics Toolbox)

Kolmogorov-Smirnov test of the distribution of one sample

Syntax

H = kstest(X)
H = kstest(X,cdf)
H = kstest(X,cdf,alpha,tail)
[H,P,KSSTAT,CV] = kstest(X,cdf,alpha,tail)

Description

H = kstest(X) performs a Kolmogorov-Smirnov test to compare the values in the data vector X with a standard normal distribution (that is, a normal distribution having mean 0 and variance 1). The null hypothesis for the Kolmogorov-Smirnov test is that X has a standard normal distribution. The alternative hypothesis that X does not have that distribution. The result H is 1 if we can reject the hypothesis that X has a standard normal distribution, or 0 if we cannot reject that hypothesis. We reject the hypothesis if the test is significant at the 5% level.

For each potential value x, the Kolmogorov-Smirnov test compares the proportion of values less than x with the expected number predicted by the standard normal distribution. The kstest function uses the maximum difference over all x values is its test statistic. Mathematically, this can be written as

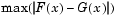
where 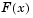is the proportion of X values less than or equal to x and 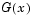is the standard normal cumulative distribution function evaluated at x.

H = kstest(X,cdf) 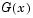compares the distribution of X to the hypothesized distribution defined by the two-column matrix cdf. Column one contains a set of possible x values, and column two contains the corresponding hypothesized cumulative distribution function values . If possible, you should define cdf so that column one contains the values in X. If there are values in X not found in column one of cdf, kstest will approximate 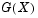by interpolation. All values in X must lie in the interval between the smallest and largest values in the first column of cdf. If the second argument is empty (cdf = []), kstest uses the standard normal distribution as if there were no second argument.

The Kolmogorov-Smirnov test requires that cdf be predetermined. It is not accurate if cdf is estimated from the data. To test X against a normal distribution without specifying the parameters, use lillietest instead.

H = kstest(X,cdf,alpha,tail) specifies the significance level alpha and a code tail for the type of alternative hypothesis. If tail = 0 (the default), kstest performs a two-sided test with the general alternative 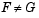. If tail = -1, the alternative is that 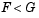. If tail = 1, the alternative is 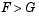. The form of the test statistic depends on the value of tail as follows.

```
tail =  0:
tail = -1:  
tail =  1:
```

[H,P,KSSTAT,CV] = kstest(X,cdf,alpha,tail) also returns the observed p-value P, the observed Kolmogorov-Smirnov statistic KSSTAT, and the cutoff value CV for determining if KSSTAT is significant. If the return value of CV is NaN, then kstest determined the significance calculating a p-value according to an asymptotic formula rather than by comparing KSSTAT to a critical value.

Examples

Example 1. Let's generate some evenly spaced numbers and perform a Kolmogorov-Smirnov test to see how well they fit to a normal distribution:

x = -2:1:4
x =
    -2    -1     0     1     2     3     4
[h,p,k,c] = kstest(x,[],0.05,0)
h =
     0
p =
      0.13632
k =
      0.41277
c =
      0.48342

We cannot reject the null hypothesis that the values come from a standard normal distribution. Although intuitively it seems that these evenly-spaced integers could not follow a normal distribution, this example illustrates the difficulty in testing normality in small samples.

To understand the test, it is helpful to generate an empirical cumulative distribution plot and overlay the theoretical normal distribution.

xx = -3:.1:5;
cdfplot(x)
hold on
plot(xx,normcdf(xx),'r--')

The Kolmogorov-Smirnov test statistic is the maximum difference between these curves. It appears that this maximum of 0.41277 occurs as we approach x = 1.0 from below. We can see that the empirical curve has the value 3/7 here, and we can easily verify that the difference between the curves is 0.41277.

```
normcdf(1) - 3/7
ans =
      0.41277
```

We can also perform a one-sided test. By setting tail = -1 we indicate that our alternative is 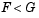, so the test statistic counts only points where this inequality is true.

[h,p,k] = kstest(x, [], .05, -1)
h =
     0
p =
     0.068181
k =
      0.41277

The test statistic is the same as before because in fac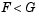t at x = 1.0. However, the p-value is smaller for the one-sided test. If we carry out the other one-sided test, we see that the test statistic changes, and is the difference between the two curves near x = -1.0.

[h,p,k] = kstest(x,[],0.05,1)
h =
     0
p =
      0.77533
k =
      0.12706
2/7 - normcdf(-1)
ans =
      0.12706

Example 2. Now let's generate random numbers from a Weibull distribution, and test against that Weibull distribution and an exponential distribution.

x = weibrnd(1, 2, 100, 1);
kstest(x, [x weibcdf(x, 1, 2)])
ans =
     0
kstest(x, [x expcdf(x, 1)])
ans =
     1

See Also

kstest2, lillietest

ksdensity kstest2