Statistics Toolbox

Response Surface Designs

Sometimes simple linear and interaction models are not adequate. For example, suppose that the outputs are defects or yield, and the goal is to minimize defects and maximize yield. If these optimal points are in the interior of the region in which the experiment is to be conducted, we need a mathematical model that can represent curvature so that it has a local optimum. The simplest such model has the quadratic form

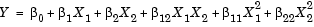
containing linear terms for all factors, squared terms for all factors, and products of all pairs of factors.

Designs for fitting these types of models are known as response surface designs. One such design is the full factorial design having three values for each input. Although the Statistics Toolbox is capable of generating this design, it is not really a satisfactory design in most cases because it has many more runs than are necessary to fit the model.

The two most common designs generally used in response surface modeling are central composite designs and Box-Behnken designs. In these designs the inputs take on three or five distinct values (levels), but not all combinations of these values appear in the design.

The functions described here produce specific response surface designs:

• Central Composite Designs
• Box-Behnken Designs

If these do not serve your purposes, consider creating a D-optimal design. For more information see D-Optimal Designs.

Fractional Factorial Designs

Central Composite Designs