chi2pdf (Statistics Toolbox)

Chi-square (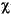²) probability density function (pdf)

Syntax

```
Y = chi2pdf(X,V)
```

Description

Y = chi2pdf(X,V) computes the 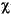² pdf at each of the values in X using the corresponding parameters in V. Vector or matrix inputs for X and V must have the same size, which is also the size of output Y. A scalar input is expanded to a constant matrix with the same dimensions as the other input.

The degrees of freedom parameters in V must be positive integers, and the values in X must lie on the interval [0 1].

The 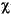² pdf for a given value x and 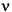degrees of freedom is

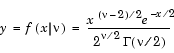
where 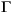( · ) is the Gamma function. The result, y, is the probability that a single observation from a 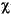² distribution with 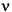degrees of freedom will have value x.

If x is standard normal, then x² is distributed 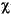² with one degree of freedom. If x₁, x₂, ..., x_n are n independent standard normal observations, then the sum of the squares of the x's is distributed 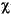²with n degrees of freedom (and is equivalent to the gamma density function with parameters 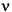/2 and 2).

Examples

nu = 1:6;
x = nu;
y = chi2pdf(x,nu)
y =
    0.2420    0.1839    0.1542    0.1353    0.1220    0.1120

The mean of the 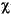² distribution is the value of the degrees of freedom parameter, nu. The above example shows that the probability density of the mean falls as nu increases.

chi2inv chi2rnd