

| Statistics Toolbox |   |
Syntax
Description
p = computes the probability that a sample, capable(data,specs)
data, from some process falls outside the bounds specified in specs, a 2-element vector of the form [lower upper].
The assumptions are that the measured values in the vector data are normally distributed with constant mean and variance and that the measurements are statistically independent.
[p,Cp,Cpk] = capable(data,specs)
Cp and Cpk.
Cp is the ratio of the range of the specifications to six times the estimate of the process standard deviation:
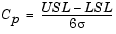
For a process that has its average value on target, a Cp of 1 translates to a little more than one defect per thousand. Recently, many industries have set a quality goal of one part per million. This would correspond to Cp = 1.6. The higher the value of Cp, the more capable the process.
Cpk is the ratio of difference between the process mean and the closer specification limit to three times the estimate of the process standard deviation:
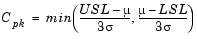
where the process mean is µ. For processes that do not maintain their average on target, Cpk is a more descriptive index of process capability.
Example
Imagine a machined part with specifications requiring a dimension to be within three thousandths of an inch of nominal. Suppose that the machining process cuts too thick by one thousandth of an inch on average and also has a standard deviation of one thousandth of an inch. What are the capability indices of this process?
data = normrnd(1,1,30,1); [p,Cp,Cpk] = capable(data,[-3 3]); indices = [p Cp Cpk] indices = 0.0172 1.1144 0.7053
We expect 17 parts out of a thousand to be out-of-specification. Cpk is less than Cp because the process is not centered.
Reference
[1] Montgomery, D., "Introduction to Statistical Quality Control," John Wiley & Sons 1991. pp. 369-374.
 | canoncorr | capaplot |  |