

| Statistics Toolbox |   |
Beta probability density function (pdf)
Syntax
Description
Y = betapdf(X,A,B)
computes the beta pdf at each of the values in X using the corresponding parameters in A and B. Vector or matrix inputs for X, A, and B must all have the same size. A scalar input is expanded to a constant matrix with the same dimensions of the other inputs. The parameters in A and B must all be positive, and the values in X must lie on the interval [0 1].
The beta probability density function for a given value x and given pair of parameters a and b is
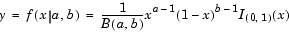
where B( · ) is the Beta function. The result, y, is the probability that a single observation from a beta distribution with parameters a and b will have value x. The indicator function 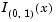 ensures that only values of x in the range (0 1) have nonzero probability. The uniform distribution on (0 1) is a degenerate case of the beta pdf where a = 1 and b = 1.
ensures that only values of x in the range (0 1) have nonzero probability. The uniform distribution on (0 1) is a degenerate case of the beta pdf where a = 1 and b = 1.
A likelihood function is the pdf viewed as a function of the parameters. Maximum likelihood estimators (MLEs) are the values of the parameters that maximize the likelihood function for a fixed value of x.
Examples
a = [0.5 1; 2 4] a = 0.5000 1.0000 2.0000 4.0000 y = betapdf(0.5,a,a) y = 0.6366 1.0000 1.5000 2.1875
See Also
betacdf, betafit, betainv, betalike, betarnd, betastat, pdf
 | betalike | betarnd |  |