| Simulink Reference | |
Library
Description
The Sine Wave block provides a sinusoid. The block can operate in either time-based or sample-based mode.
Time-Based Mode
The output of the Sine Wave block is determined by
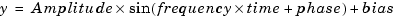
Time-based mode has two submodes: continuous mode or discrete mode. The value of the Sample time parameter determines whether the block operates in continuous mode or discrete mode:
0 (the default) causes the block to operate in continuous mode.
>0 causes the block to operate in discrete mode.
See Specifying Sample Time in the online documentation for more information.
Using the Sine Wave Block in Continuous Mode
A Sample time parameter value of 0 causes the block to operate in continuous mode. When operating in continuous mode, the Sine Wave block can become inaccurate due to loss of precision as time becomes very large.
Using the Sine Wave Block in Discrete Mode
A Sample time parameter value greater than zero causes the block to behave as if it were driving a Zero-Order Hold block whose sample time is set to that value.
Using the Sine Wave block in this way allows you to build models with sine wave sources that are purely discrete, rather than models that are hybrid continuous/discrete systems. Hybrid systems are inherently more complex and as a result take longer to simulate.
The Sine Wave block in discrete mode uses an incremental algorithm rather than one based on absolute time. As a result, the block can be useful in models intended to run for an indefinite length of time, such as in vibration or fatigue testing.
The incremental algorithm computes the sine based on the value computed at the previous sample time. This method makes use of the following identities:
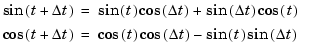
These identities can be written in matrix form:
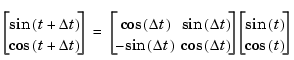
Since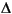 
t is constant, the following expression is a constant:
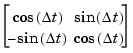
Therefore the problem becomes one of a matrix multiplication of the value of sin(t) by a constant matrix to obtain sin(t+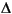t).
Discrete mode reduces but does not eliminate accumulation of roundoff errors. This is because the computation of the block's output at each time step depends on the value of the output at the previous time step.
Sample-Based Mode
Sample-based mode uses the following formula to compute the output of the Sine Wave block.
A is the amplitude of the sine wave.
p is the number of time samples per sine wave period.
k is a repeating integer value that ranges from 0 to p-1.
o is the offset (phase shift) of the signal.
b is the signal bias.
In this mode, Simulink sets k equal to 0 at the first time step and computes the block's output, using the preceding formula. At the next time step, Simulink increments k and recomputes the output of the block. When k reaches p, Simulink resets k to 0 before computing the block's output. This process continues until the end of the simulation.
The sample-based method of computing the block's output does not depend on the result of the previous time step to compute the result at the current time step. It therefore avoids roundoff error accumulation. However, it has one potential drawback. If the block is in a conditionally executed subsystem and the conditionally executed subsystem pauses and then resumes execution, the output of the Sine Wave block might no longer be in sync with the rest of the simulation. Thus, if the accuracy of your model requires that the output of conditionally executed Sine Wave blocks remain in sync with the rest of the model, you should use time-based mode for computing the output of the conditionally executed blocks.
Parameter Dimensions
The block's numeric parameters must be of the same dimensions after scalar expansion. If the Interpret vector parameters as 1-D option is off, the block outputs a signal of the same dimensions and dimensionality as the parameters. If the Interpret vector parameters as 1-D option is on and the numeric parameters are row or column vectors (i.e., single row or column 2-D arrays), the block outputs a vector (1-D array) signal; otherwise, the block outputs a signal of the same dimensionality and dimensions as the parameters.
Data Type Support
A Sine Wave block accepts and outputs real signals of type double.
Parameters and Dialog Box
1.1 rad/s. This parameter appears only if you choose time-based as the Sine type of the block.0 radians. This parameter appears only if you choose time-based as the Sine type of the block.0. If the sine type is sample-based, the sample time must be greater than 0. See Specifying Sample Time in the online documentation for more information.If selected, column or row matrix values for the Sine Wave block's numeric parameters result in a vector output signal; otherwise, the block outputs a signal of the same dimensionality as the parameters. If this option is not selected, the block always outputs a signal of the same dimensionality as the block's numeric parameters.
Characteristics
| Sample Time |
Continuous, discrete, or inherited for time-based and discrete for sample-based |
| Scalar Expansion |
Of parameters |
| Dimensionalized |
Yes |
| Zero Crossing |
No |
| | Signal Specification | Slider Gain | |