

| Signal Processing Toolbox |   |
Upsample, apply an FIR filter, and downsample
Syntax
Description
upfirdn performs a cascade of three operations:
xin by a factor of the integer p (inserting zeros)
h
q (throwing away samples)
upfirdn has been implemented as a MEX-file for maximum speed, so only the outputs actually needed are computed. The FIR filter is usually a lowpass filter, which you must design using another function such as remez or fir1.
Note
The function resample performs an FIR design using firls, followed by rate changing implemented with upfirdn.
|
yout filters the input signal = upfirdn(xin,h)
xin with the FIR filter having impulse response h. If xin is a row or column vector, then it represents a single signal. If xin is a matrix, then each column is filtered independently. If h is a row or column vector, then it represents one FIR filter. If h is a matrix, then each column is a separate FIR impulse response sequence. If yout is a row or column vector, then it represents one signal. If yout is a matrix, then each column is a separate output. No upsampling or downsampling is implemented with this syntax.
yout specifies the integer upsampling factor = upfirdn(xin,h,p)
p, where p has a default value of 1.
yout specifies the integer downsampling factor = upfirdn(xin,h,p,q)
q, where q has a default value of 1.
Note
Since upfirdn performs convolution and rate changing, the yout signals have a different length than xin. The number of rows of yout is approximately p/q times the number of rows of xin.
|
Remarks
Usually the inputs xin and the filter h are vectors, in which case only one output signal is produced. However, when these arguments are arrays, each column is treated as a separate signal or filter. Valid combinations are:
xin with h. The output signal yout is a row vector if xin is a row; otherwise, yout is a column vector.
h with each column of xin. The resulting yout will be an matrix with the same number of columns as xin.
h with xin. The resulting yout will be an matrix with the same number of columns as h.
xin and h. The resulting yout is an matrix with the same number of columns as xin and h.
Examples
If both p and q are equal to 1 (that is, there is no rate changing), the result is ordinary convolution of two signals (equivalent to conv):
This example implements a seven-channel filter bank by convolving seven different filters with one input signal, then downsamples by five:
Implement a rate change from 44.1 kHz (CD sampling rate) to 48 kHz (DAT rate), a ratio of 160/147. This requires a lowpass filter with cutoff frequency at 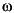 c = 2
c = 2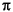 /160:
/160:
% Design lowpass filter with cutoff at 1/160th of fs. hh=fir1(300,2/160); % Need a very long lowpass filter yy=upfirdn(xx,hh,160,147);
In this example, the filter design and resampling are separate steps. Note that resample would do both steps as one.
Algorithm
upfirdn uses a polyphase interpolation structure. The number of multiply-add operations in the polyphase structure is approximately (LhLx-pLx)/q where Lh and Lx are the lengths of h[n] and x[n], respectively.
A more accurate flops count is computed in the program, but the actual count is still approximate. For long signals x[n], the formula is often exact.
Diagnostics
If p and q are large and do not have many common factors, you may see this message:
Instead, you should use an interpolation function, such as interp1, to perform the resampling and then filter the input.
See Also
conv, decimate, downsample, filter, interp, intfilt, resample, upsample
References
[1] Crochiere, R.E., and L.R. Rabiner, Multi-Rate Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1983, pp. 88-91.
[2] Crochiere, R.E., "A General Program to Perform Sampling Rate Conversion of Data by Rational Ratios," Programs for Digital Signal Processing, IEEE Press, New York, 1979, pp. 8.2-1 to 8.2-7.
 | unwrap | upsample |  |