Signal Processing Toolbox

besself

Bessel analog filter design

Syntax

• [b,a] = besself(n,Wn)
  [b,a] = besself(n,Wn,'ftype')
  [z,p,k] = besself(...)
  [A,B,C,D] = besself(...)
  

Description

besself designs lowpass, bandpass, highpass, and bandstop analog Bessel filters. Analog Bessel filters are characterized by almost constant group delay across the entire passband, thus preserving the wave shape of filtered signals in the passband. Digital Bessel filters do not retain this quality, and besself therefore does not support the design of digital Bessel filters.

[b,a] = besself(n,Wn) designs an order n lowpass analog filter with cutoff frequency Wn. It returns the filter coefficients in the length n+1 row vectors b and a, with coefficients in descending powers of s, derived from this transfer function:

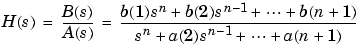
Cutoff frequency is the frequency at which the magnitude response of the filter begins to decrease significantly. For besself, the cutoff frequency Wn must be greater than 0. The magnitude response of a Bessel filter designed by besself is always less than 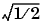at the cutoff frequency, and it decreases as the order n increases.

If Wn is a two-element vector, Wn = [w1 w2] with w1 < w2, then besself(n,Wn) returns an order 2*n bandpass analog filter with passband w1 < 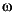 < w2.

[b,a] = besself(n,Wn,'ftype') designs a highpass or bandstop filter, where the string 'ftype' is

• 'high' for a highpass analog filter with cutoff frequency Wn
• 'stop' for an order 2*n bandstop analog filter if Wn is a two-element vector, Wn = [w1 w2]. The stopband is w1 < 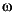 < w2.

With different numbers of output arguments, besself directly obtains other realizations of the analog filter. To obtain zero-pole-gain form, use three output arguments as shown below.

[z,p,k] = besself(n,Wn) or

[z,p,k] = besself(n,Wn,'ftype') returns the zeros and poles in length n or 2*n column vectors z and p and the gain in the scalar k.

To obtain state-space form, use four output arguments as shown below:

[A,B,C,D] = besself(n,Wn) or

[A,B,C,D] = besself(n,Wn,'ftype') where A, B, C, and D are

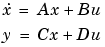
and u is the input, x is the state vector, and y is the output.

Examples

Design a fifth-order analog lowpass Bessel filter that suppresses frequencies greater than 10,000 rad/s and plot the frequency response of the filter using freqs:

• [b,a] = besself(5,10000);
  freqs(b,a)                 % Plot frequency response
  
  
  

Limitations

Lowpass Bessel filters have a monotonically decreasing magnitude response, as do lowpass Butterworth filters. Compared to the Butterworth, Chebyshev, and elliptic filters, the Bessel filter has the slowest rolloff and requires the highest order to meet an attenuation specification.

For high order filters, the state-space form is the most numerically accurate, followed by the zero-pole-gain form. The transfer function coefficient form is the least accurate; numerical problems can arise for filter orders as low as 15.

Algorithm

besself performs a four-step algorithm:

1. It finds lowpass analog prototype poles, zeros, and gain using the besselap function.
2. It converts the poles, zeros, and gain into state-space form.
3. It transforms the lowpass filter into a bandpass, highpass, or bandstop filter with desired cutoff frequencies using a state-space transformation.
4. It converts the state-space filter back to transfer function or zero-pole-gain form, as required.

See Also

besselap, butter, cheby1, cheby2, ellip

besselap

bilinear