Signal Processing Toolbox

Delay

The group delay of a filter is a measure of the average delay of the filter as a function of frequency. It is defined as the negative first derivative of a filter's phase response. If the complex frequency response of a filter is 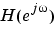, then the group delay is

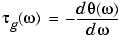
where 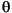is the phase angle of 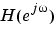. Compute group delay with

• [gd,w] = grpdelay(b,a,n)
  

which returns the n-point group delay, 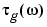, of the digital filter specified by b and a, evaluated at the frequencies in vector w.

The phase delay of a filter is the negative of phase divided by frequency:

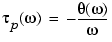
To plot both the group and phase delays of a system on the same graph, type

• [b,a] = butter(10,200/1000);
  gd = grpdelay(b,a,128);
  [h,f] = freqz(b,a,128,2000);
  pd = -unwrap(angle(h))*(2000/(2*pi))./f;
  plot(f,gd,'-',f,pd,'--')
  axis([0 1000 -30 30])
  legend('Group Delay','Phase Delay')
  
  
  

Magnitude and Phase

Zero-Pole Analysis